131 résultats trouvés
Revenir à la recherche avancée
Et il y a quelque chose qui me gêne : si w_{n+2}=w_n , alors w_{2p} = w_0 Et donc en comparant avec l'expression de w_0 , on a la condition : d-s_0-a = s_0+a d=2(s_0+a) cos(2 \pi \frac{b}{c})= 1-(s_0+a) D'une part, 0 \le s_0+a \le 2 Et d'autre part : 2 \pi \frac{b}{c} = +/- a...
- 02 Aoû 2013, 21:32
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de périodicité
- Réponses: 13
- Vues: 1085
Parce que d ne dépend pas de n... w_{n} = v_{n} \, \sqrt{1 \,+\, \left( {d-s_{n}-a \over z_{n}} \right)^2} Comme v_{n+2}=v_n , s_{n+2}=s_n et z_{n+2}=z_n Alors, w_{n+2} = v_{n+2} \, \sqrt{1 \,+\, \left( {d-s_{n+2}-a \over z_{n+2}} \right)^2} = v_{n} \, \sqrt{1 \,+\, \left( {d-s_{...
- 02 Aoû 2013, 21:20
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de périodicité
- Réponses: 13
- Vues: 1085
- 02 Aoû 2013, 19:19
- Forum: ✎✎ Lycée
- Sujet: [TS+] Lostounet en MPSI
- Réponses: 42
- Vues: 2118
Alors j'ai fait les calculs et je trouve : s_{2p}=s_0 s_{2p+1}=\frac{s_0 a^2}{s_0^2+z_0^2} z_{2p}=z_0 z_{2p+1}=\frac{z_0 a^2}{s_0^2+z_0^2} v_{2p}=v_0 v_{2p+1}=\frac{v_0 a}{\sqrt{s_0^2+z_0^2}} Ces trois suites sont "périodiques de période 2" ( u_{n+2}=u_n ) Donc w_n aussi, ie w_{n+2}=w_n qu...
- 02 Aoû 2013, 17:50
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de périodicité
- Réponses: 13
- Vues: 1085
Ok donc il suffit d'expliciter s_n pour finir car on a \frac{s_{n+1}}{s_n}=\frac{z_{n+1}}{z_n}=\frac{{v_{n+1}}^2}{{v_n}^2} Tu remarques d'abord qu'il existe k (à déterminer) telle que z_n=k s_n , puis qu'il existe K (aussi à déterminer) telle que s_{n+1}s_n = K Donc en prenant les termes paires / im...
- 02 Aoû 2013, 16:11
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de périodicité
- Réponses: 13
- Vues: 1085
- 02 Aoû 2013, 15:44
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de périodicité
- Réponses: 13
- Vues: 1085
Salut,
Quand tu dis :
 est quelconque ou fonction de
est quelconque ou fonction de 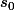 et
et  ?
?
Quand tu dis :
Et cela à partir des conditions initiales où,
(et donc
) sont quelconques mais :
- 02 Aoû 2013, 14:22
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de périodicité
- Réponses: 13
- Vues: 1085
Salut,
La droite que tu cherches est linéaire, y=ax avec a coefficient directeur.
Et le coeff dir (ou pente) est égal à la tangente de l'angle (tu peux le voir par la formule du coeff).
Donc l'équation sera :
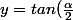x)
La droite que tu cherches est linéaire, y=ax avec a coefficient directeur.
Et le coeff dir (ou pente) est égal à la tangente de l'angle (tu peux le voir par la formule du coeff).
Donc l'équation sera :
- 01 Aoû 2013, 14:10
- Forum: ✎✎ Lycée
- Sujet: équation de la bissectrice d'un angle
- Réponses: 2
- Vues: 1503
- 01 Aoû 2013, 13:00
- Forum: ✎✎ Lycée
- Sujet: [TS+] Lostounet en MPSI
- Réponses: 42
- Vues: 2118
Bonjour,
En effet, tu n'as qu'à prendre C=3 et tu démontres par récurrence.
Une petite astuce pour C=3 : démontre que à partir de n=1
à partir de n=1
Après comme) , tu auras ton résultat
, tu auras ton résultat
En effet, tu n'as qu'à prendre C=3 et tu démontres par récurrence.
Une petite astuce pour C=3 : démontre que
Après comme
- 01 Aoû 2013, 09:39
- Forum: ✎✎ Lycée
- Sujet: [TS+] Lostounet en MPSI
- Réponses: 42
- Vues: 2118
- 31 Juil 2013, 14:40
- Forum: ✯✎ Supérieur
- Sujet: [optimisation sous contraintes, non lineaire]
- Réponses: 8
- Vues: 1047
- 30 Juil 2013, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Cherche relation de récurence
- Réponses: 9
- Vues: 637
Oui comme le dit Sourire_banane, somme des p^k avec les coef de Pascal (décalés d'un rang par contre)
- 30 Juil 2013, 16:17
- Forum: ✯✎ Supérieur
- Sujet: Cherche relation de récurence
- Réponses: 9
- Vues: 637
Quel sont les coefficients du triangle de Pascal ?
La réponse ne va pas te tomber dessus sans effort !!!
Au moins pas de ma part !!!
La réponse ne va pas te tomber dessus sans effort !!!
Au moins pas de ma part !!!
- 30 Juil 2013, 15:42
- Forum: ✯✎ Supérieur
- Sujet: Cherche relation de récurence
- Réponses: 9
- Vues: 637
- 30 Juil 2013, 13:10
- Forum: ✯✎ Supérieur
- Sujet: Cherche relation de récurence
- Réponses: 9
- Vues: 637
- 30 Juil 2013, 12:49
- Forum: ✯✎ Supérieur
- Sujet: Cherche relation de récurence
- Réponses: 9
- Vues: 637
- 26 Juil 2013, 12:47
- Forum: ✯✎ Supérieur
- Sujet: Suite et équivalent
- Réponses: 5
- Vues: 521
- 26 Juil 2013, 11:14
- Forum: ✯✎ Supérieur
- Sujet: Suite et équivalent
- Réponses: 5
- Vues: 521
- 26 Juil 2013, 11:01
- Forum: ✯✎ Supérieur
- Sujet: Suite et équivalent
- Réponses: 5
- Vues: 521
Positif ? Non. Mais non nul pour a dans R oui (cela revient au même je te l'accorde).
Discriminant négatif et on peut diviser
Discriminant négatif et on peut diviser
- 26 Juil 2013, 10:04
- Forum: ✎✎ Lycée
- Sujet: Inégalité du réordonnement
- Réponses: 6
- Vues: 603
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
