33 résultats trouvés
Revenir à la recherche avancée
Équation différentielle
Bonjour tout le monde, j'ai rencontré un petit souci pour résoudre une partie de cette équation : Y' + 2Y' + Y = e^x Alors pour la partie gauche j'ai trouvé, r^2 + 2r +1 , donc le discriminant est = 0 donc solution unique -b/2a donc, r1 = r2 = -1 , donc Ys(x) = (Ax+B)e^{-1x} ...
- 10 Mai 2014, 15:17
- Forum: ✯✎ Supérieur
- Sujet: Équation différentielle
- Réponses: 2
- Vues: 328
pour que p dans notre cas soit une lois de probabilité elle doit vérifier : - p est une application de IN dans [0,1] . - p(IN)=1 . - p(\cup_{i \in I}A_i)=\cup_{i\in I}p(A_i) pour toute famille finie ou dénombrable d'éléments disjoints A_i,{i \in I} de IN . p(IN)=1 ca...
- 10 Oct 2013, 15:38
- Forum: ✯✎ Supérieur
- Sujet: Probabilité
- Réponses: 5
- Vues: 557
arnaud32 a écrit:que doit verifier une loi de probabilite?
la nature de la variable ? J'ai pas trop l'idée de ce qu'elle vérifie .. :help:
- 09 Oct 2013, 16:43
- Forum: ✯✎ Supérieur
- Sujet: Probabilité
- Réponses: 5
- Vues: 557
Probabilité
Bonjour, j'ai une question que je n'arrive pas à résoudre :
On considère un réel a appartenant à ]0,1[.
Montrer que l'on définit une loi de probabilité d'une variable aléatoire X à une valeur dans N en posant : quelque soit n appartenant à N=(1-a)a^n)
On considère un réel a appartenant à ]0,1[.
Montrer que l'on définit une loi de probabilité d'une variable aléatoire X à une valeur dans N en posant : quelque soit n appartenant à N
- 09 Oct 2013, 16:30
- Forum: ✯✎ Supérieur
- Sujet: Probabilité
- Réponses: 5
- Vues: 557
Luc a écrit:Euh, pourquoiserait égal à
?
Et bien, vu sue c'est sur
- 21 Juin 2013, 15:21
- Forum: ✯✎ Supérieur
- Sujet: Fonction à deux variables
- Réponses: 9
- Vues: 674
Bonjour, attention aux parenthèses, leur placement change complètement le sens de ce que tu écris. Pour calculer la dérivée partielle de f par rapport à x1, il faut considérer f comme une fonction d'une variable (ici, x1), en laissant x2 constant et en appliquant les formules usuelles de dérivation...
- 17 Juin 2013, 17:21
- Forum: ✯✎ Supérieur
- Sujet: Fonction à deux variables
- Réponses: 9
- Vues: 674
salut pour la dérivée par rapport à x_2 , c'est \fra{ -2x_1 x_2}{1+x_{1}^2+x_{1}^2 , je pense Oui c'est ca que j'ai trouvé !!! Mais c'est juste alors ? Parce que si c'est le cas, j'ai abandonné pour rien... Je me disais que ca semblait vraiment pas juste alors j'ai pas continué à chercher les point...
- 17 Juin 2013, 17:17
- Forum: ✯✎ Supérieur
- Sujet: Fonction à deux variables
- Réponses: 9
- Vues: 674
Fonction à deux variables
Bonjour à tous, je viens de passer mes partiels de maths et j'ai un petit doute concernant les réponses que j'ai apporté ... Voici l'énoncé Soit la fonction réelle f à deux variables réelles définie par : Y=f(x) = f(x1 ; x2) = x1/ ( 1+x1^2 +x2^2) ..... calculer les partielles...
- 17 Juin 2013, 16:05
- Forum: ✯✎ Supérieur
- Sujet: Fonction à deux variables
- Réponses: 9
- Vues: 674
Bon il y a un moment où il faut arrêter de pleurer et lire l'énoncé . f(x)=2x pour x \in [0,a], cela signifie que f est nulle en dehors. L'intégrale sur R vaut 1 signifie \int_0^a 2x dx = 1 donc a = ... Le calcul de l'espérance et de la variance est une application directe du cours (à un calcul d'i...
- 14 Juin 2013, 18:59
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et densité
- Réponses: 9
- Vues: 538
Bon il y a un moment où il faut arrêter de pleurer et lire l'énoncé . f(x)=2x pour x \in [0,a], cela signifie que f est nulle en dehors. L'intégrale sur R vaut 1 signifie \int_0^a 2x dx = 1 donc a = ... Le calcul de l'espérance et de la variance est une application directe du cours (à un calcul d'i...
- 14 Juin 2013, 16:42
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et densité
- Réponses: 9
- Vues: 538
Sylviel a écrit:Pourquoi veux tu mettre la densité d'une loi gaussienne ??? :mur:
Relis ton énoncé et tu as ta densité donnée explicitement...
..
une densité est une fonction :
- positive
- dont l'intégrale sur R vaut 1.
2*1 ?? puisque
- 14 Juin 2013, 16:29
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et densité
- Réponses: 9
- Vues: 538
Bonjour, une densité est une fonction : - positive - dont l'intégrale sur R vaut 1. Pour calculer l'espérance de X de densité f il faut calculer \int xf(x)dx Je te laisse faire les deux premières questions avec àça. il faut donc que j'utilise la formule de densité 1/(;)-racine de 2*pi) * e^...
- 14 Juin 2013, 16:15
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et densité
- Réponses: 9
- Vues: 538
Probabilité et densité
Bonjour, je suis bloquée, j'espère trouver une réponse ici. Merci d'avance !! :we: :we: Alors, voiçi l'énoncé : I Soit X la variable continue de densité fX(x) = 2x pour x appartient (0, a). 1) Montrer que fX est bien une densité pour une valeur de a positive à déterminer. 2) Calcule...
- 14 Juin 2013, 15:31
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et densité
- Réponses: 9
- Vues: 538
Bonjour, Tu sais que ln(x) est défini pour x appartenant à ]0; +oo[ . Il te suffit donc d'étudier le signe de x1x2 + e > 0 pour trouver l'ensemble de définition de la fonction f. [CENTER] x1 x2 + e > 0 __ x1x2 > -e ____ x1 > -e/x2 ___ et ___ x2 > -e/x1 ?[/CENTER]
- 13 Juin 2013, 13:07
- Forum: ✎✎ Lycée
- Sujet: domaine de définition de Ln
- Réponses: 5
- Vues: 460
domaine de définition de Ln
Déterminer l'ensemble de définition de la fonction f
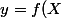 = f(x1;x2) = 1/3 [ln(x1x2+e)^2]^3)
Merci d'avance ! :we: :we:
Merci d'avance ! :we: :we:
- 13 Juin 2013, 12:59
- Forum: ✎✎ Lycée
- Sujet: domaine de définition de Ln
- Réponses: 5
- Vues: 460
XENSECP a écrit:Embêtant ce...
Edit : tu peux peut-être t'inspirer de : http://math1.unice.fr/~diener/MAB0809/S2COURS4.pdf ?
Dérivées partielles => gradient => ligne de niveau orthogonale au gradient...
Merci :we:
- 13 Juin 2013, 12:55
- Forum: ✯✎ Supérieur
- Sujet: Courbe de niveau
- Réponses: 3
- Vues: 816
Courbe de niveau
[CENTER] Donner l'expression générale des courbes de niveau de la fonction f. avec f(x;y) = 2x^4 +y^2 - 12xy J'ai donc égalisé avec 2x^4 +y^2 - 12xy = q mais ensuite, je bloque :help: ... je sais pas comment il faut que je réduise c'est à dire quand est-ce que j'aurai répondu à la question ....
- 12 Juin 2013, 19:19
- Forum: ✯✎ Supérieur
- Sujet: Courbe de niveau
- Réponses: 3
- Vues: 816
Malheureusement, ça me dit vraiment rien .. :/ J'ai pensée le résoudre par (x-1)^2 = 4 ce qui me donne x= 3 et y = 1 mais ensuite quand je les remplacent, ça me donne pas 0 mais -2 .. Aah non c'est bon j'ai trouvé... C'était pourtant simple, il suffit que je remplace x dans l'équation et je...
- 12 Juin 2013, 16:30
- Forum: ✎✎ Lycée
- Sujet: Équation à deux inconnus
- Réponses: 5
- Vues: 456
Archibald a écrit:Donc, du type^2+(y-a)^2=r^2)
ça ne te dit vraiment rien ?
Malheureusement, ça me dit vraiment rien .. :/
J'ai pensée le résoudre par
ce qui me donne
et
mais ensuite quand je les remplacent, ça me donne pas 0 mais -2 ..
- 12 Juin 2013, 16:26
- Forum: ✎✎ Lycée
- Sujet: Équation à deux inconnus
- Réponses: 5
- Vues: 456
Équation à deux inconnus
Bonjour tout le monde, j'ai une équation à deux inconnus que je n'arrive pas à résoudre pouvez vous m'aidez ? Merci d'avance :we:
[CENTER]
4-[(x-1)²+(y+1)²]=0 [/CENTER]
[CENTER]
4-[(x-1)²+(y+1)²]=0 [/CENTER]
- 12 Juin 2013, 16:15
- Forum: ✎✎ Lycée
- Sujet: Équation à deux inconnus
- Réponses: 5
- Vues: 456
- 33 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
