Forum de Mathématiques: Maths-Forum

Bonsoir, c'est pas évident deviner quel genre de réponse on attend pour la 3ème question, mais une remarque importante est que la relation de récurrence fait intervenir des petits coefficients, qui ne vont donc pas être efficaces pour "mélanger" les chiffres de X_n et produire l'illusion ...

les nombres générés n'ont rien d'aléatoire,simplement quand on fait des statistiques sur eux, on obtient des lois et des résultats semblables à ceux obtenus sur une famille de nombres aléatoires. Oui, oui. Erratum. Je voulais dire pseudo-aléatoire. Et donc quelle interprétation pensez-vous que l'on...

X_{n+2} = (6 X_{n+1} - 9 X_n ) mod m c'est juste Comment peut-on interpréter ce résultat ? X_n étant un générateur de nombre entier aléatoire, est-ce correct de dire que cette équation montre que l'on peut deviner tout les nombres aléatoires qui vont être générés à partir de deux entiers su...

Pour Q1, on va décomposer en 2 questions. Q1a) calculer a² Q1b) calculer a² mod m Je n'ai pas l'impression que ta réponse soit correcte. a^2 = 2^{32} + 3 \times 2 \times 2^{16} + 9 a^2 = 2 \times 2^{31} + 3 \times 2 \times 2^{16} + 9 a^2 mod m = ( \cancelto{0}{2 \times 2^{31}} + 3 \times 2 \tim...

Bonjour à tous, J'étudie les générations pseudo-aléatoires de nombre entiers et je bloque sur une question de partiel : Soit X_n le générateur définit par : X_{n+1} = a \times X_n mod m avec a = 65539 = 2^{16} +3 et m = 2^{31} Q1) Caculer a^2 mod m Q2) Déduire une équation donnant X_{n+2} en fonctio...

Bonjour,

http://www.les-mathematiques.net/b/e/l/node3.php

Je comprend pas trop ce que tu veut dire. Mais j'ai déja trouvé ce que je cherchais avec ce topic. Il voulait simplement expliquer qu'une constante (en multiplication) peut "entrer" et "sortir" de la somme sans que cela produise un changement. Par exemple : \sum_{k=1}^{n}{2k} = ...

Bonsoir,

C'est une multiplication, par exemple :

Merci pour ton EDIT qui donne des éléments de contexte intéressants. Et donc, qu'est-ce qui te manque maintenant ? Je voulais un brin de précision quant à la formule de I_n et si elle était convergente. Quant à la convergence j'ai bien eu ma réponse. Je creuse encore pour savoir si l'on peut encore...

Bonsoir,

Algèbre et analyse : cours de mathématiques de première année avec exercices corrigés / Stéphane Balac, Frédéric Sturm

Bonne continuation.

Sa Majesté a écrit:

Math3matiqu3 a écrit:Simplement pour dire n tend vers +oo

Si tu veux mais "est ce que converge ?" suffit.

J'avoue

Le tri proposé dans la vidéo s'appelle "tri par sélection", tu peux te documenter sur
https://fr.wikipedia.org/wiki/Tri_par_s%C3%A9lection

Est il possible de simplifier cette formule ? I_n = \frac{n!}{\prod_{k=0}^{n}{(k + \frac{3}{2})}} Si on veut : I_n=\dfrac{2^{2n+2} \cdot n! \cdot (n+1)!}{(2n+3)!} Est ce que I_n converge pour n suffisament grand ? Question étrange : que vient faire "pour n suffisament g...

Bonjour, Est il possible de simplifier cette formule ? I_n = \frac{n!}{\prod_{k=0}^{n}{(k + \frac{3}{2})}} Est ce que I_n converge pour n suffisament grand ? Merci. EDIT : La formule est tirée de cet exo : Pour tout entier n , on pose : I_n = \int_{0}^{1}{x^n\sqrt{1-x} dx} 1. En calculant I_...

Bonsoir, Calculer l'intégrale : \int_{0}^{\pi} \frac{x sin(x)}{1 + cos(x)}\, \mathrm{d}x Par changement de variable t = (\frac{x}{2}) , on aura : x -> 0 \implies t-> 0 et x -> \pi \implies t-> + \infty x = 2 arctg(t) \implies dx = \frac{2}{1+t^2} dt sin(x) = \...

ça a été fait un peu plus tôt dans l'énoncé, est positive et est strictement croissante sur son domaine de définition.

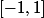La fonction est définie dans , donc ?

En tout les cas, la fonction réciproque n'est pas définie en !

Bonsoir, f(x) = \frac{2}{1-sin(x)} - 2 Soit g , la fonction réciproque de f. Montrer que g est dérivable sur R , et que g'(x) = \frac{1}{(2+x) \sqrt{x+1}} Je trouve g(x) = arcsin(\frac{x}{x+2}) et je trouve bel et bien g'(x) mais je ne ...

Merci !

Bonsoir à tous ! Soit p\geq 2 un entier naturel premier. On suppose qu'il existe a \in Z tel que : 9a^2 + 15a + 7 \equiv 0 [p] a) Montrer que p \geq 5 . b) Prouver que (3a + 2)^3 \equiv 1 [p] c) En déduire que : (3a + 2) \wedge p = 1 De l'aide s'il vous plaît ? Je n'ai même pas trouv...