27 résultats trouvés
Revenir à la recherche avancée
je sais que je t'embêtes mais si tu pouvais m'aider rapidement ça m'arrangerais mais merci quand même

- par hakka
- 23 Fév 2013, 17:37
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Parce que la limite l de la suite (u_n) est en fait le nombre e. A la rigueur tu peux l'admettre. Tu peux lire ceci : http://fr.wikipedia.org/wiki/E_%28nombre%29 j'ai une autre question a te demander stp de l'aide avec toi je comrpends bien :) il faut que je prouves que Un<ou égal a Wn comm...
- par hakka
- 22 Fév 2013, 15:48
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Carpate a écrit:C'est la limite de

quand
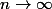
je ne comprends pas pourquoi tu dis que UN et Vn converge vers e
- par hakka
- 20 Fév 2013, 18:02
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Je reformule : Les suites (u_n) et (v_n) sont adjacentes et tendent vers la même limite : e Cette limite sera atteinte à 10{-6} près si w_n= u_n-v_n qui représente l'écart de (u_n) avec e est \leq 10{-6} ce qui est réalisé pour le rang n de développement de (u_n) tel que \frac{1}{nn...
- par hakka
- 20 Fév 2013, 15:28
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Il faudrait quand même que tu lises ton cours ! (u_n) croît et (v_n) décroît u_n -v_n= \frac{1}{nn!} \rightarrow 0 quand n \rightarrow +\infty Les suites (u_n) et (v_n) sont adjacentes et convergent toutes les 2 vers une limite : l (qui n'est autre que e) Pour n > 1 ...
- par hakka
- 20 Fév 2013, 12:33
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Il faudrait quand même que tu lises ton cours ! (u_n) croît et (v_n) décroît u_n -v_n= \frac{1}{nn!} \rightarrow 0 quand n \rightarrow +\infty Les suites (u_n) et (v_n) sont adjacentes et convergent toutes les 2 vers une limite : l (qui n'est autre que e) Pour n > 1 ...
- par hakka
- 19 Fév 2013, 12:37
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
v_{n+1}-v_{n}=u_{n+1}-u_{n}+\frac{1}{(n+1)(n+1)!}-\frac{1}{nn!}=\frac{1}{(n+1)!}+\frac{1}{(n+1)(n+1)!}-\frac{1}{nn!} \frac{1}{(n+1)!}+\frac{1}{(n+1)(n+1)!}=\frac{n+1+1}{(n+1)(n+1)!}=\frac{n+2}{(n+1)(n+1)...
- par hakka
- 19 Fév 2013, 09:23
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Carpate a écrit:!}]- [1 + \frac{1}{1!} + ... +\frac{1}{n!}]=\frac{1}{(n+1)!})
donc positif
)
croît
Est-ce
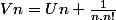
ou
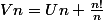
?
C'est
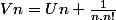
- par hakka
- 18 Fév 2013, 22:14
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Carpate a écrit:Ecris l'expression de
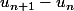
que tu as obtenu
j'ai 1/n(n+1) pour Un+1-Un donc c'est bon car N(n+1)!>0 car nN* mais pour Vn+1-Vn je vois pas du tous tu pourrais pas me passer la piste a suivre et j'essayerai de faire le développement ?
- par hakka
- 18 Fév 2013, 21:35
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Bonsoir, Ca ne sert à rien de demander de l'aide sans préciser ce que tu as fait et ce qui te bloque ! Comment veux-tu qu'on t'aide alors, sauf à faire l'exercice à ta place Toutes les questions me bloque enfaite je sais juste que pour la première il faut faire Un+1-Un et Vn+1-Vn mais mon résultat ...
- par hakka
- 18 Fév 2013, 21:18
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Bonjour je n'arrive pas a mon exercice si vous pouviez m'aidez : soit Un=+1/1!+1/2!+....+1/n! et Vn=Un+1/n*n! a)Montrer que U est croissante et V est décroissante b)Un<ou egal Vn en déduire la convergence des suites 2a)On pose Wn= Vn-Un a) jusqtifier que 0<Wn<ou egal 1/n 3)justifier que U et v conve...
- par hakka
- 18 Fév 2013, 20:51
-
- Forum: ✎✎ Lycée
- Sujet: Etude de Suite
- Réponses: 18
- Vues: 1066
Deluxor a écrit:Bonsoir
hakka,
a) Pour montrer que la suite
)
est croissante calcule :
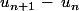
. Que trouves-tu?
je trouve 1/n(n+1)! or N(n+1)!>0 car nN* mais je suis pas sur :S et Vn+1-Vn je n'y arrives pas....
- par hakka
- 18 Fév 2013, 09:55
-
- Forum: ✎✎ Lycée
- Sujet: étude de suite
- Réponses: 4
- Vues: 593
j'ai réussis a prouver que Un+1-Un était croissante mais pas que VN+1-Vn est décroissante de l'aide svp :)
- par hakka
- 18 Fév 2013, 09:53
-
- Forum: ✎✎ Lycée
- Sujet: étude de suite
- Réponses: 4
- Vues: 593
On a vu que p \begin{pmatrix} n \\ p \end{matrix} = \frac{n!}{(p-1)!(n-p)!} . et là tu as : n \begin{pmatrix} n-1 \\ p-1 \end{matrix} = n \frac{n-1!}{(p-1)!(n-p)!} . = \frac{n!}{(p-1)!(n-p)!} . Donc tu as bien l'égalité Ah j'ai compris bas merci pour ...
- par hakka
- 17 Fév 2013, 21:15
-
- Forum: ✎✎ Lycée
- Sujet: démontrer des Coefficients binomiaux
- Réponses: 25
- Vues: 1605
Idril51 a écrit:n (n-1)! = ? On l'a déjà vu avant.
oui mais je vois pas comment lié les truc entre eux frenchement sa me prends la tete
- par hakka
- 17 Fév 2013, 20:47
-
- Forum: ✎✎ Lycée
- Sujet: démontrer des Coefficients binomiaux
- Réponses: 25
- Vues: 1605
Idril51 a écrit:Ensuite tu fais pareil en partant de : n

.
=n
!}{(n-p)!(p-1)!})
.
Et là normalement tu devrais réussir a trouver
euh non je vois pas désolé :S
- par hakka
- 17 Fév 2013, 20:26
-
- Forum: ✎✎ Lycée
- Sujet: démontrer des Coefficients binomiaux
- Réponses: 25
- Vues: 1605
Ok, alors : p \begin{pmatrix} n \\ p \end{matrix} = \frac{pn!}{p!(n-p)!} . Là tu as remplacé p parmi n , par la formule donnée au début. Et là, tu as le terme p/p! dans la fraction. Et p/p! = p / (1x2x....xp) = 1/(1x2x3x...xp-1) = 1/(p-1)!. Donc tu obtiens : = \frac{n!}{(p-1)!(n...
- par hakka
- 17 Fév 2013, 20:13
-
- Forum: ✎✎ Lycée
- Sujet: démontrer des Coefficients binomiaux
- Réponses: 25
- Vues: 1605
Bonjour je n'arrive pas a mon exercice si vous pouviez m'aidez : soit Un=+1/1!+1/2!+....+1/n! et Vn=Un+1/n*n! a)Montrer que U est croissante et V est décroissante b)Un<ou egal Vn en déduire la convergence des suites 2a)On pose Wn= Vn-Un a) jusqtifier que 0<Wn<ou egal 1/n 3)justifier que U et v conve...
- par hakka
- 17 Fév 2013, 19:50
-
- Forum: ✎✎ Lycée
- Sujet: étude de suite
- Réponses: 4
- Vues: 593
Donc pour la 3ème : p \begin{pmatrix} n \\ p \end{matrix} = p \frac{n!}{p!(n-p)!} = \frac{n!}{(p-1)!(n-p)!} . Et tu pars de n \begin{pmatrix} n-1 \\ p-1 \end{matrix} . Tu fais pareil, tu utilises la formule, tu simplifies et tu retombes sur \frac{n!}{(p-1)!(n-p&#...
- par hakka
- 17 Fév 2013, 19:30
-
- Forum: ✎✎ Lycée
- Sujet: démontrer des Coefficients binomiaux
- Réponses: 25
- Vues: 1605
est en fait le nombre e. A la rigueur tu peux l'admettre.
