je veux inserer se maillage [HTML]http://www.4shared.com/file/fLJSkxz7/CreateUniformMeshMASTER.html?[/HTML]
dans ce programme [HTML]http://www.4shared.com/file/NHEZ9blO/fem2d_heat.html?[/HTML]
le dossier complet se trouve ici :
[HTML]http://www.4shared.com/rar/enIUF2PW/fem2d_heat.html?[/HTML]
23 résultats trouvés
Revenir à la recherche avancée
[quote="Ariane2557"]Bonsoir,
J'ai quelques difficultés avec un changement de variables:
j'ai Z = X² + Y² et théta = Arctg(Y/X) avec (-pi/2 Y=Xtg(théta)
Alors
et mtn tu pe continué comme ça
J'ai quelques difficultés avec un changement de variables:
j'ai Z = X² + Y² et théta = Arctg(Y/X) avec (-pi/2 Y=Xtg(théta)
Alors
et mtn tu pe continué comme ça
- 04 Avr 2013, 19:41
- Forum: ✯✎ Supérieur
- Sujet: Changement de variables avec des coordonnées polaires
- Réponses: 10
- Vues: 2169
Bonjour. Je suis en économie et Gestion, et j'ai un petit souci. En mathématiques, on a une partie sur les vecteurs, et j'ai quelques zones qui sont bien floues. En gros, voilà les questions que je me pose, sur lesquelles j'espere, vous pourrez m'éclairer: -Est ce qu'une famille à n+1 vecteurs dans...
- 21 Mar 2013, 17:01
- Forum: ✯✎ Supérieur
- Sujet: Les vecteurs (génératrice, bases...)
- Réponses: 1
- Vues: 554
exercice sur les distributions
Montrer quil existe )
telle que = 1) avec
avec 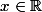
telle que
- 17 Mar 2013, 23:30
- Forum: ✯✎ Supérieur
- Sujet: exercice sur les distributions
- Réponses: 10
- Vues: 794
Bonjour, j'aimerais avoir de l'aide sur un exercice : Dans cette question, on utilisera que la ;) de k=1 jusquà N de k = N(N+1)/2 Calculer ;) de k=1 jusqu'a n de (2k+1) Donc j'ai juste remplacé donc j'obtient : ;) k=1 jusqu'à n (2N(N+1))/2 -1 = ;) N(N+1)-1 Mais je ne vois pas quoi faire de plus, s...
- 28 Fév 2013, 18:32
- Forum: ✯✎ Supérieur
- Sujet: Dm sur les sommes
- Réponses: 8
- Vues: 714
il suffit de montrer que si V appartient a vect(u1,u2,u3) alors (u1,u2,u3,v) est une famille liéé :) est ça c'est facille a montrer :)
- 28 Fév 2013, 13:29
- Forum: ✯✎ Supérieur
- Sujet: Dm Algebre Linéaire
- Réponses: 7
- Vues: 754
pour montrer que U_n est est majoré par 2 c simple . pour n=0 on a U_0=1<2 par recurrence on va supposer que U_n<2 est on montre que U_{n+1}<2 U_n<2 alors 1+U_n<3 sqrt{1+U_n}<sqrt{3}<2 alors U_{n+1}<2 pour la 2ém queston on a U_n croissante est majoré alors la suite est convergente vert un element ...
- 25 Fév 2013, 23:40
- Forum: ✯✎ Supérieur
- Sujet: exercice sur les suites
- Réponses: 4
- Vues: 536
on montre d'abord que la suite est croissante donc un>=1 2-un+1=2-V(1+un)=[4-(1+un)]/[2+V(1+un)] u00 donc Un+1<2 pour montrer que U_n est est majoré par 2 c simple . pour n=0 on a U_0=1<2 par recurrence on va supposer que U_n<2 est on montre que U_{n+1}<2 U_n<2 alors 1+U_n<3 sqrt{1+U_n}<sqrt{3}<2 a...
- 25 Fév 2013, 23:35
- Forum: ✯✎ Supérieur
- Sujet: exercice sur les suites
- Réponses: 4
- Vues: 536
- 23 Fév 2013, 15:06
- Forum: ✯✎ Supérieur
- Sujet: Statistique binomiale et loi poisson
- Réponses: 2
- Vues: 914
mliebert a écrit:Je ne comprends pas pourquoi nln(1+(1/n)) tend vers 1 en +oo. Pour moi je trouve 0
nn c'est 1 car
- 23 Fév 2013, 14:51
- Forum: ✯✎ Supérieur
- Sujet: Limite en exponientielle
- Réponses: 4
- Vues: 424
c'est la decomposition des fractions tu dois lire le cours " D'ecomposition des
fractions rationnelles"
fractions rationnelles"
- 23 Fév 2013, 14:46
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'intégrales
- Réponses: 9
- Vues: 521
Prouver que Pn=(1+(1/n))PUISSANCE(n) tend vers exponentielle p_n=(1+\frac{1}{n})^n alors ln(p_n)=ln((1+\frac{1}{n})^n)= n ln((1+\frac{1}{n}) la limite de n ln((1+\frac{1}{n}) c'est 1 alore lim de ln P_n=1 ==> que P_n tend vers e
- 23 Fév 2013, 14:37
- Forum: ✯✎ Supérieur
- Sujet: Limite en exponientielle
- Réponses: 4
- Vues: 424
- 23 Fév 2013, 14:29
- Forum: ✯✎ Supérieur
- Sujet: Determinaison d'une limite dans N
- Réponses: 7
- Vues: 701
U_n=\frac{n-\sqrt{n^2 +1}}{n+sqrt{n^2 +1}}=-(n-\sqrt{n^2 +1})^2 c ça !! U_n=\frac{n-\sqrt{n^2 +1}}{n+sqrt{n^2 +1}}=\frac{n(1-\sqrt{1 +\frac{1}{n^2}})}{n(1+sqrt{1 +\frac{1}{n^2}})}=\frac{1-\sqrt{1 +\frac{1}{n^2}}}{1+sqrt{1 +\frac{1}{n^2}}} Mtn c sinple a calculer la lim c'est 0
- 23 Fév 2013, 14:21
- Forum: ✯✎ Supérieur
- Sujet: Determinaison d'une limite dans N
- Réponses: 7
- Vues: 701
- 23 Fév 2013, 14:13
- Forum: ✯✎ Supérieur
- Sujet: Determinaison d'une limite dans N
- Réponses: 7
- Vues: 701
Pour a tu peux pas procéder comme tu l'as fait par contre si tu étudies la limite en l'infini de t*(t/(t^3 - 3t + 2)) de deux manières tu peux trouver directement la valeur de A ! A= -c il sufit de faire l'equation (x-1)(\frac{A}{x-1}+\frac{b}{(x-1)^2}+\frac{c}{x+1})=(x-...
- 23 Fév 2013, 13:58
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'intégrales
- Réponses: 9
- Vues: 521
jlb a écrit:x+1>x-1: tu peux peut-être étudier le sens de variations de t--->e^t/t?
le domaine de deffinition c'est ]-inf,-1[ou ]-1,1[ou],1+inf [
ou
alors tu pe ke f' est negative sure ]-inf,1[ zt positive sur l'autre intervale.
- 23 Fév 2013, 13:30
- Forum: ✯✎ Supérieur
- Sujet: Etude des variations d'une intégrale
- Réponses: 6
- Vues: 2182
Oui je crois que A=B+I4 et donc A²=4(B+I4) pour une première expression mais pour une deuxième je ne vois pas trop, ce serait A²= (B+I4)² ? Et donc 4(B+I4)=(B+I4)² équivaut à 4B+4I=B²+2BI+I². Je crois que I²=I et 2BI=2B Donc on aurait 4B+4I=B²+2B+I équivaut à B²-2B=3I équivaut à B(B-2)=3I équivaut ...
- 23 Fév 2013, 02:39
- Forum: ✯✎ Supérieur
- Sujet: Matrices
- Réponses: 3
- Vues: 436
on peut faire la demarche suivante :) on va poser f(x)=Ax et f'(x)=A'x pour A injective 'il existe une unique solution du problème ça est simple il suffit de prendre deux solution x,y et on montre que x=y (f et f' sont injective) mtn la deusieme on a f est f' injective ==> f rond f' injective n'est ...
- 21 Fév 2013, 13:12
- Forum: ✯✎ Supérieur
- Sujet: matrices et unicité d'une solution
- Réponses: 20
- Vues: 1776
c simple pour montrer que f est ijectif on doit montre ça f(x)=f(x')==>x=x'!!
(on a g rond f ingectif :) <==> pour tout x est y g rond f(x)=g rondf(y) ==> x=y )
Alors f(x)=f(x')==>g rond f(x)=g rondf(x") ==>x=x'
(on a g rond f ingectif :) <==> pour tout x est y g rond f(x)=g rondf(y) ==> x=y )
Alors f(x)=f(x')==>g rond f(x)=g rondf(x") ==>x=x'
- 21 Fév 2013, 02:34
- Forum: ✯✎ Supérieur
- Sujet: Composée grondf injective alors f injective
- Réponses: 3
- Vues: 1159
- 23 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
