Forum de Mathématiques: Maths-Forum

ta validé? moi c Anas E.
normalement ya mon nom dans la liste de ceux qui ont réussi

Kikoo <3 Bieber a écrit:92 ??? Moi j'avais trouvé 93 (

93 cest juste, mais fo enlever le coefficient de x^8, regarde bien la question

Kikoo <3 Bieber a écrit:Enlève les trois petits points.

c fait. la réponse est 92
jai fnii tout les exercices, et je suis lvl 4 en tout, en une semaine (le
temps minimal est 15 jours) merci tout le mooonde

essaye 92, parceque le coefficient de x^8 nest pas conté

PS: çA MARCHE!!!
merci tt le monde

Chan, tu peux donner ta methode pour trouver ces valeurs stp? (étape par étape)

Kikoo <3 Bieber a écrit:Je me suis inscrit sur ce site et je suis tombé sur le même problème ^^ Pas facile, c'est là où je vais bloquer.

PS : si j'essaye avec tes valeurs, Chan, ça marche pô :hein:

parceque jai changé les valeurs de lexo

Salut C'est mon avis aussi On montre facilement en élevant au carré à plusieurs reprises que \sqrt{5+\sqrt{2}+\sqrt{7}} est solution de x^8-20x^6+132x^4-320x^2+200=0 les autres solutions étant: - \sqrt{5+\sqrt{2}+\sqrt{7}} , \sqrt{5-\sqrt{2}+\sqrt{7}} , - \sqrt{5-\sqrt{2}+\sqrt{7}} , \sqrt{5-\sqrt{...

Alors tu continues à élever au carré après avoir fait ce qu'il faut et tu vas voir disparaître toutes les racines . Personnellement je ne vois pas l'intérêt de l'exercice ou bien une évidence m'a échappé . Imod la racine reste toujours quand on met puissance n'importe quel nombre, il ya toujours un...

Alors ce problème n'est pas de ton niveau :zen: Il te manque plein de connaissances pour donner du sens à l'exercice . Imod jai fini le programme de cette année et de celle de l'année suivante, et jai trouvé cet exercice sur http://www.brilliant.org , cest selon les niveaux en maths en général, pas...

Le_chat a écrit:Non il n'y a plus de racines, il faut utiliser (sqrt(2)+sqrt(7))^2=9+sqrt(56)

oui mais il ya toujours sqrt(14), mais selon la question, le résultat doit être naturel, donc plus AUCUNE racine

Imod

je suis en seconde.
et je suis allé jusqu'au bout, mais il ya toujours des racine

et bieber,
oui le coefficiant de x_8 est 1 (polynome monique )

oui, mais la reponse dans ce cas contiens des racines, donc n'est pas un nombre naturel

et jai oublié de préciser (dsl jai oublié) que le résultat est un nombre naturel entre 0 et 999 (inclusif)

oui mais ce sera de degré 4, nous on veux un de degré 8.
il sera possible de le mettre puissance 4, mais je ne crois pas que le résultat de sigma(0;7) |a_i| sera le même, je crois qu on doit trouver le polynomial minimum qui remplit les conditions

Imod a écrit:Si on note alors il est facile de calculer puis et ainsi de suite , on trouve un polynôme de degré 8 dont est une racine .

Imod

salut, mais elle est où la variable?

salut
non, vu que tout ces nombre sont des racines carrées, mais le probleme est que je ne suis pas que cest correct, parceque la somme de 8racines nest surement pas un nombre rationnel

salut
jai détérminé les 8 racines du polynome, mais me fo maintenant trouver les coefficient, et ça va être long

comme ça cest de plus en plus compliqué. la c simple parcequ on travaille avec 2 multiplications seulement. si tu veux trouver les autres coefficients, tu devrais avoir 8 multiplications, donc un nombre en fonction de 7 autres, é cest pas pratique. moi jai essayé de trouvé une fonction de 4em degré ...

oui, cest le coefficient de x^8 (noter que n=8)

soit p(x) = sigma(0;8) a_i x^î un polynome de degré 8, avec a_n=1 et et pour tout i, a_i qui appartien a Z
calculer |a_1|+|a_2|...|a_7| sachant que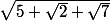 est une racine de p