34 résultats trouvés
Revenir à la recherche avancée
Ah okey merci ! Donc il faut toujours que X vaut 0 et que P(0) = 0 pour que ça marche ? (ainsi que ses dérivées jusqu'à n-1)
- 17 Juil 2014, 00:29
- Forum: ✯✎ Supérieur
- Sujet: Polynome divisibilité
- Réponses: 16
- Vues: 1037
si a est racine double du polynome P, alors a est racine de P'. Si a est racine double de P, Si t'écris P(x)=(x-a)^alpha*Q(x), (donc avec alpha>1) avec Q qui n'a pas a pour racine, alors si tu dérives P'(x)=alpha(x-a)^(alpha -1)Q(x)+Q'(x)(x-a)^alpha = (x-a)^(alpha-1)(alpha Q(x)+Q'(x)(x-a)^alpha et ...
- 16 Juil 2014, 19:18
- Forum: ✯✎ Supérieur
- Sujet: Polynome divisibilité
- Réponses: 16
- Vues: 1037
Je viens de recevoir la correction, la voici pour la 2ème:
Notons Q(x) = divise (
divise (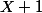^n -nX-1) . On montre que Q(0) = 0 et il faut faire la même chose pour Q'(0) = 0 Quelqu'un peut m'expliquer pourquoi on dérive ?
. On montre que Q(0) = 0 et il faut faire la même chose pour Q'(0) = 0 Quelqu'un peut m'expliquer pourquoi on dérive ?
Notons Q(x) =
- 16 Juil 2014, 16:27
- Forum: ✯✎ Supérieur
- Sujet: Polynome divisibilité
- Réponses: 16
- Vues: 1037
- 16 Juil 2014, 15:24
- Forum: ✎✎ Lycée
- Sujet: Logarithme simplification
- Réponses: 4
- Vues: 605
- 16 Juil 2014, 08:21
- Forum: ✯✎ Supérieur
- Sujet: Polynome divisibilité
- Réponses: 16
- Vues: 1037
Salut! A mon avis, il doit au moins y avoir deux erreures dans ta donnée. Primo, tu n'as aucun "x" dans la formule de base, alors que ta réponse en contient... Ce que je veux dire, c'est que: e^{\frac{ln(x)^2}{2}}=sqrt{e^{ln(2)}}=sqrt{2} Il n'y a aucune inconnue! Deuxio, i...
- 16 Juil 2014, 08:14
- Forum: ✎✎ Lycée
- Sujet: Logarithme simplification
- Réponses: 4
- Vues: 605
Polynome divisibilité
Bonjour je fais un exercice sur les polynôme mais je ne comprends pas comment on s'y prend pour le faire
Voici l'exercice : Montrer (sans récurrence) que divise
divise ^{2n}-1)
 divise (
divise (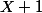^n -nX-1) et que
et que
^2) divise
divise X^n +1)
Voici l'exercice : Montrer (sans récurrence) que
- 16 Juil 2014, 00:30
- Forum: ✯✎ Supérieur
- Sujet: Polynome divisibilité
- Réponses: 16
- Vues: 1037
Logarithme simplification
Bonjour il y a quelque chose que je ne comprends pas.
J'ai^2}{2}}) (c'est une puissance) et en le simplifiant on trouve
(c'est une puissance) et en le simplifiant on trouve
}}) Quelqu'un peut m'expliquer comment on a simplifié ?
Quelqu'un peut m'expliquer comment on a simplifié ?
J'ai
- 16 Juil 2014, 00:23
- Forum: ✎✎ Lycée
- Sujet: Logarithme simplification
- Réponses: 4
- Vues: 605
\lim_{x \to 0} \frac{ln(1-x)}{x} = \lim_{y \to 1} \frac{ln(y)}{1-y} ensuite tu appliques ce que viens de te proposer L.A. (tu peux aussi le faire sans le changement de variable si tu le vois directement)... Je vois donc ça fait référence au taux de variation cette limite vaut donc f...
- 02 Mai 2013, 15:03
- Forum: ✎✎ Lycée
- Sujet: Limite en 0 de ln(1-x)/x
- Réponses: 5
- Vues: 6996
- 01 Mai 2013, 14:01
- Forum: ✎✎ Lycée
- Sujet: Limite en 0 de ln(1-x)/x
- Réponses: 5
- Vues: 6996
Limite en 0 de ln(1-x)/x
Bonjour je cherche la limite en 0 de ln(1-x)/x mais je trouve que la limite est en 0 est de 1 en utilisant lexponentielle or la limite en 0 de cette fonction est en -1 sur Géogébra, quelqu'un peut-il m'expliquer comment trouver le -1 ?
- 01 Mai 2013, 13:11
- Forum: ✎✎ Lycée
- Sujet: Limite en 0 de ln(1-x)/x
- Réponses: 5
- Vues: 6996
- 01 Mai 2013, 13:08
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité d'une fonction
- Réponses: 10
- Vues: 719
Ce sont pourtant de simples fonctions polynomiales, elles sont continues et dérivables sur \mathbb{R} . Je peux savoir quelle formule as-tu utilisée, et surtout qu'est-ce que tu en as compris ? J'ai utilisé la 1ère formule : \lim_{x \to a}\frac{f(x)-f(a)}{x-a} . De ce que j'ai compr...
- 30 Avr 2013, 00:13
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité d'une fonction
- Réponses: 10
- Vues: 719
Pas très rigoureuse comme conclusion... Je vois pas vraiment comme l'améliorer, mais mon concours se base seulement sur des QCM donc je pense pas que ça m'aidera si je conclu ou non. Sinon pourrais-tu m'aider pour celui là ? Je n'arrive pas vraiment à le résoudre \left\{ \begin{array} f(x) ...
- 29 Avr 2013, 19:55
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité d'une fonction
- Réponses: 10
- Vues: 719
f'(0)= \lim_{h \to 0} \frac{f(0+h)-f(0)}{h} = \lim_{h \to 0} \frac{(0+h)|0+h| - 0|0|}{h} = \lim_{h \to 0} \frac{h|h|}{h} = \lim_{h \to 0} |h| Qu'en conclues-tu ? J'en conclus que \lim_{h \to 0} |h| tend vers 0 et donc que la fonction est bien dérivable en 0 c'est...
- 29 Avr 2013, 11:12
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité d'une fonction
- Réponses: 10
- Vues: 719
Merci de ton aide donc pour mon exemple j'ai utilisé la 1ère formule et je tombe sur  = 0 c'est bien ça ?
= 0 c'est bien ça ?
- 28 Avr 2013, 23:02
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité d'une fonction
- Réponses: 10
- Vues: 719
Dérivabilité d'une fonction
Bonjour je vais bientôt passer un concours et je voudrais connaître une méthode pour savoir si une fonction est dérivable en 0 ou non.
Par exemple comment savoir si f(x) = x|x| est dérivable en 0
Par exemple comment savoir si f(x) = x|x| est dérivable en 0
- 28 Avr 2013, 21:53
- Forum: ✎✎ Lycée
- Sujet: Dérivabilité d'une fonction
- Réponses: 10
- Vues: 719
- 08 Jan 2013, 18:28
- Forum: ✎✎ Lycée
- Sujet: Fonction logarithme
- Réponses: 7
- Vues: 457
- 08 Jan 2013, 18:07
- Forum: ✎✎ Lycée
- Sujet: Fonction logarithme
- Réponses: 7
- Vues: 457
Il résulte de l'étude des variations de f(x) qu'elle admet, sur ]0;+\infty[ , un maximum nul (en x = 1) donc f(x) \leq 0 K merci et pour le 3b. avec le changement de variable j'obtiens : ln (\frac{1}{x}) \geq (\frac{1}{x})-1 = ln \leq \frac{\frac{1}{x}-1}{x} car ln (\frac{1}...
- 08 Jan 2013, 18:02
- Forum: ✎✎ Lycée
- Sujet: Fonction logarithme
- Réponses: 7
- Vues: 457
- 34 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
