100 résultats trouvés
Revenir à la recherche avancée
- 05 Juin 2014, 11:52
- Forum: ✯✎ Supérieur
- Sujet: Matrice / algébre
- Réponses: 4
- Vues: 508
je n'arrive pas à déterminer les matrice réelles orthogonale
j'ai dit que Gl4(R) inter L était un sous algèbre
j'ai dit que Gl4(R) inter L était un sous algèbre
- 05 Juin 2014, 08:53
- Forum: ✯✎ Supérieur
- Sujet: Matrice / algébre
- Réponses: 4
- Vues: 508
Matrice / algébre
bonsoir http://img15.hostingpics.net/pics/416511matrice2.jpg je bloque quand on me demande de calculer la matrice inverse de M(a,b) j'ai montrée qu'elle était inversible grâce aux déterminant de sa matrice semblable D(a,b) faut-il utiliser la matrice semblable D(a,b) pour le calculer la matrice inve...
- 27 Mai 2014, 22:09
- Forum: ✯✎ Supérieur
- Sujet: Matrice / algébre
- Réponses: 4
- Vues: 508
Dénombrement I
Bonsoir
je souhaite trouver le nombre de permutations de nombre pair sur pair sur {1,2,3,4,5,6,7,8,9,10,11,12}
je trouve que c'est 6! c'est ça ?
car on fait une permutation de 6 nombre pair
je souhaite trouver le nombre de permutations de nombre pair sur pair sur {1,2,3,4,5,6,7,8,9,10,11,12}
je trouve que c'est 6! c'est ça ?
car on fait une permutation de 6 nombre pair
- 12 Mai 2014, 20:00
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement I
- Réponses: 1
- Vues: 261
que veux tu calculer exactement ?
la somme des k(k + 1) de k = 0 jusqu'à n ?
la somme de k(k-1) de 2 à n
- 11 Mai 2014, 09:37
- Forum: ✯✎ Supérieur
- Sujet: Sommes
- Réponses: 12
- Vues: 668
on a aussi
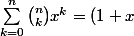^n)
en dérivant 2 fois et en posant x = 1 on a
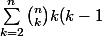=n(n-1)(1+1)^{n-2}=n(n-1)2^{n-2))
cela voudrait dire que pour n => 2 ou bien je suis à l'ouest ?
pour n => 2 ou bien je suis à l'ouest ?
en dérivant 2 fois et en posant x = 1 on a
cela voudrait dire que
- 10 Mai 2014, 19:28
- Forum: ✯✎ Supérieur
- Sujet: Sommes
- Réponses: 12
- Vues: 668
Merci pour votre aide je l'ai trouvé avec la récurrence finalement je me suis rendu compte que la suite que j'avais au début n'était pas la vraie somme car on U_n=(n+1)(n+2) et la somme de k(k-1) de 2 à n vaut u_0+u_1+u_2+u_3+u_4....+u_(n-2) et la suite qui traduit la somme e...
- 10 Mai 2014, 17:32
- Forum: ✯✎ Supérieur
- Sujet: Sommes
- Réponses: 12
- Vues: 668
Sommes
bonjour je souhaite calculer la sommes des k(k-1) pour k allant de 2 à n sans passer par k^2-k ( car on me demande d'en déduire k² ensuite ) la somme vaut = 2 + 6 + 12 + 20 + 30 + 42 .... pour passer de 2 de à 6 on ajoute 4 et de 6 à 12 on ajoute 6 puis 8 puis 10 etc j'en déduit une suite : U_n+1=U_...
- 10 Mai 2014, 13:38
- Forum: ✯✎ Supérieur
- Sujet: Sommes
- Réponses: 12
- Vues: 668
soit A = a b c d comme f est une endomorphisme de M2(K) le determinant de f dans la base canonique est : det(F)= det ( F(E1),F(E2),F(E3),F(E4)) F(E1)= A.E1= a 0 c 0 de même on trouve que : F(E2) F(E3) 0 a b 0 0 c d 0 puis F(E4) 0 b 0 d donc on obtient la matrice 4x4 : a 0 b 0 0 a 0 b c 0 d 0 0 c 0 d...
- 13 Avr 2014, 19:09
- Forum: ✯✎ Supérieur
- Sujet: Determinant
- Réponses: 5
- Vues: 431
- 13 Avr 2014, 13:19
- Forum: ✯✎ Supérieur
- Sujet: Determinant
- Réponses: 5
- Vues: 431
Determinant
salut, K un corps . Soient A dans M2(K),soit f lapplication de M2(K) dans lui-même dé;)ni par : f(M)=AM. Montrer que, dans les bases canoniques : det(f)=(det A)^2 . je vois pas comment faire .. det(f)=det(AM)=Det(A)Det(M) faudrait que je montrer que M vaut A dans l'endomorphisme de M2(K) ?
- 13 Avr 2014, 10:05
- Forum: ✯✎ Supérieur
- Sujet: Determinant
- Réponses: 5
- Vues: 431
Bonjour ,
656353=16*41022+1
et 267^{16} = 1 modulo(17) [petit théorème de Fermat ]
tu remplaces 656353 dans 267^{656353}-12 puis tu fais le calcul modulo 17.
656353=16*41022+1
et 267^{16} = 1 modulo(17) [petit théorème de Fermat ]
tu remplaces 656353 dans 267^{656353}-12 puis tu fais le calcul modulo 17.
- 08 Mar 2014, 10:01
- Forum: ✯✎ Supérieur
- Sujet: Divisibilité
- Réponses: 3
- Vues: 386
avec la relation entre racines et coefficients , on a la somme des racines d'un polynomes qui vaut

Donc c'est
Merci pour votre aide Bonne soirée..
Donc c'est
Merci pour votre aide Bonne soirée..
- 07 Mar 2014, 21:53
- Forum: ✯✎ Supérieur
- Sujet: Somme
- Réponses: 2
- Vues: 278
Somme
Bonsoir ,
je n'arrive pas à calculer la somme :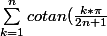^{2})
C'est la somme des racines d'un polynôme=\sum_{k=0}^{n}\binom{2n+1}{2k+1} (-1)^{k}X^{2(n-k)})
si quelqu'un a une piste svp
je n'arrive pas à calculer la somme :
C'est la somme des racines d'un polynôme
si quelqu'un a une piste svp
- 07 Mar 2014, 19:54
- Forum: ✯✎ Supérieur
- Sujet: Somme
- Réponses: 2
- Vues: 278
- 19 Jan 2014, 20:17
- Forum: ✯✎ Supérieur
- Sujet: Développement limité
- Réponses: 6
- Vues: 508
- 02 Jan 2014, 18:28
- Forum: ✯✎ Supérieur
- Sujet: Restrictions
- Réponses: 10
- Vues: 558
on pose x'=x et x=0 donc |h(0)-h(x)| \leq |0-x| pour x \geq 0 -x est positif donc |-x|= -x et comme h est croissante alors pour x\leq0 h(0) \geq h(x) donc h(0)-h(x) \geq 0 donc h(0)-h(x) \geq x h(x)-h(0) \leq x h(x&#...
- 02 Jan 2014, 18:13
- Forum: ✯✎ Supérieur
- Sujet: Restrictions
- Réponses: 10
- Vues: 558
Bonjour, Pour la question sur l'équivalence, tu ne peux pas montrer que \forall x \in \mathbb{R}, h(x) = x à partir de la croissante de h (ça serait assez contradictoire vu que tu supposes \forall x \in \mathbb{R}, h(x) > x ). En revanche tu peux montrer quelque chose de similaire q...
- 02 Jan 2014, 15:43
- Forum: ✯✎ Supérieur
- Sujet: Restrictions
- Réponses: 10
- Vues: 558
- 02 Jan 2014, 14:10
- Forum: ✯✎ Supérieur
- Sujet: Restrictions
- Réponses: 10
- Vues: 558
Salut, est-ce que ce serait possible que tu expliques comment tu obtiens ce résultat ? la fonction h est croissante et [a,b] est un segment (a = 0 et h(b)-h(a)>=0 avec linégalité de l'énoncée : |h(b)-h(a)|>=|b-a| (le cas a-b=b-a comme h([a,b]) est inclus dans [a,b] , l'intervalle est stable par h ...
- 02 Jan 2014, 01:21
- Forum: ✯✎ Supérieur
- Sujet: Restrictions
- Réponses: 10
- Vues: 558
- 100 résultats trouvés - Page 1 sur 5 • 1, 2, 3, 4, 5
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
