29 résultats trouvés
Revenir à la recherche avancée
Re: Paradoxe de Simpson (2e partie)
Merci Pseuda ! Voilà exactement l'article qui répond à mes questions (sans lever le paradoxe ! ça serait trop facile, un bon paradoxe ne se laisse pas dompter si facilement !). Merci donc, et ça me rassure sur mes intuitions mathématiques ;-) La distinction yeux-clairs/yeux-foncés de l'exemple donné...
- 03 Juin 2016, 06:30
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Re: Paradoxe de Simpson (2e partie)
Oui, en évitant les fractions, ça réduit déjà par deux le nombre de variables, et donc d'inconnues 
Je me penche sur le problème dès que j'ai fini mes paquets de copies (heureusement qu'en vrai, je n'ai pas fait deux sujets A et B pour mon interro !!!
 )
)
Je me penche sur le problème dès que j'ai fini mes paquets de copies (heureusement qu'en vrai, je n'ai pas fait deux sujets A et B pour mon interro !!!

 )
)- 30 Mai 2016, 17:45
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Re: Paradoxe de Simpson (2e partie)
Ma question ultime, en fin de compte, c'est : Etant données deux fractions \frac{M}{N} et \frac{m}{n} telles que \frac{M}{N}>\frac{m}{n} peut-on toujours trouver quatre fractions \frac{a}{b} , \frac{c}{d} , \frac{A}{B} , \frac{C}{D} avec \frac{a}{b}<\frac{A}{B} et \:\frac{c}{d}<\frac{C}{D} et telles...
- 29 Mai 2016, 21:02
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Re: Paradoxe de Simpson (2e partie)
c'est ça qui est super.Le principe d'un paradoxe c'est de te filer le vertige. Bah, ok, mais autant les paradoxes style menteur ou Achille, je m'étais habitué depuis tout petit (ça me semble même plus très intéressant). Mais découvrir à 45 balais qu'avec des toutes bêtes fractions de niveau 5e, je ...
- 29 Mai 2016, 18:35
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Re: Paradoxe de Simpson (2e partie)
Je suis bien d'accord avec toi, Beagle : j'ai effectivement inventé ma situation (mais elle pourrait néanmoins être un vrai résultat, je veux dire un résultat qui correspondrait à une vraie mise en situation). C'est bien pour ça que je dis qu' il ne peut pas y avoir de facteur de confusion (" b...
- 29 Mai 2016, 17:02
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Re: Paradoxe de Simpson (2e partie)
Désolé, je me suis encore un peu trompé, ce post aurait dû faire partie du forum "Salon Mathématiques", et pas "Collège et Primaire", mais je ne sais pas déplacer un sujet...
- 29 Mai 2016, 09:37
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Re: Paradoxe de Simpson (2e partie)
Je sais que le paradoxe de Simpson se produit lorsqu'il y a un facteur de confusion , autrement dit, dans le cas qui nous occupe, une corrélation entre le sexe d'un candidat et le choix du sujet , A ou B . Cependant, j'ai construit mon exemple complètement artificiellement, à partir de ce graphique ...
- 29 Mai 2016, 08:51
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Paradoxe de Simpson (2e partie)
Paradoxe de Simpson Dans une classe de 31 élèves, on propose un examen de fin d'année en maths, avec 2 sujets au choix : le sujet A et le sujet B . Voici les résultats de réussite en fonction des sujets A et B et du sexe des candidats : Simpson-min.jpg Il est clair que les filles ont bien mieux réu...
- 29 Mai 2016, 07:39
- Forum: ⚜ Salon Mathématique
- Sujet: Paradoxe de Simpson (2e partie)
- Réponses: 27
- Vues: 2811
Ce problème, tel que tu as présenté l'énoncé, est typiquement de niveau collège (c'est un prof de maths du secondaire qui parle). Pour ta gouverne ;-) Tu as corrigé le \frac{7}{40} , mais ta solution n'en reste pas moins erronée, car ici, les fractions \frac{5}{8} et \frac{7}{40} ne doivent pas être...
- 29 Nov 2012, 07:48
- Forum: ✎ Collège et Primaire
- Sujet: Problème de billes
- Réponses: 8
- Vues: 1432
3) a) L'aire d'un trapèze est : A = \frac{(B + b) \times h}{2} où : B et b sont les 2 bases parallèles (ici AD et BE) et h est la hauteur (ici AB). Avec les données de la figure (que tu n'as pas fournie, mais on peut se la représenter) : AD = AC = x BE = BC = 6 - x AB = 6 b) Pour l'aire du t...
- 28 Nov 2012, 23:29
- Forum: ✎✎ Lycée
- Sujet: Exercice mathématiques seconde?
- Réponses: 3
- Vues: 952
- 28 Nov 2012, 22:20
- Forum: ✎✎ Lycée
- Sujet: Comment comparer avec le signe de la différence ?
- Réponses: 5
- Vues: 702
Ici, il serait peut-être plus pertinent d'étudier :
}{f(x)}) qui vaut
qui vaut  pour
pour 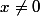 .
.
>f(x)) équivaut à
équivaut à }{f(x)}) >1 (pour les valeurs positives)
>1 (pour les valeurs positives)
Pareil pour les autres comparaisons...
Pareil pour les autres comparaisons...
- 28 Nov 2012, 22:08
- Forum: ✎✎ Lycée
- Sujet: Comment comparer avec le signe de la différence ?
- Réponses: 5
- Vues: 702
Bonsoir, si tu n'as pas de question plus précise sur cet exercice qui comporte au moins 6 questions distinctes, tu ne vas pas trouver beaucoup d'aide, ici-bas... En tout cas personne qui résoudra l'exercice pour toi, écrira la solution et la postera ici. Par contre, si tu nous dis ce que tu as déjà ...
- 28 Nov 2012, 21:18
- Forum: ✎✎ Lycée
- Sujet: Exercice mathématiques seconde?
- Réponses: 3
- Vues: 952
Tout à fait, nodjim a raison, et dans le cas de 16h40, la petite aiguille est entre le 4 et le 5, mais elle a déjà parcouru les deux tiers de son chemin entre le 4 et le 5 (40 minutes représentent les 2/3 d'une heure...) Or 1 espace = 30° comme l'a expliqué Lostounet, 2/3 d'un espace = ... ° qu'il f...
- 28 Nov 2012, 20:20
- Forum: ✎ Collège et Primaire
- Sujet: Défi de proportionnalité
- Réponses: 5
- Vues: 659
Autant que m'emporte le vent !
http://www.langue-fr.net/spip.php?article14
J'avais déjà lu quelque chose sur ça, mais ça m'était sorti de la tête.
Au temps en rire qu'en pleurer
http://www.langue-fr.net/spip.php?article14
J'avais déjà lu quelque chose sur ça, mais ça m'était sorti de la tête.
Au temps en rire qu'en pleurer
- 28 Nov 2012, 18:43
- Forum: ✎ Collège et Primaire
- Sujet: DM n°5 Niveau 3 ième - équations
- Réponses: 5
- Vues: 812
Bonjour
Je fais les mêmes calculs que la mouette, par contre, je ne trouve pas que Pierre se trompe (ni Anne, en effet).
Je fais les mêmes calculs que la mouette, par contre, je ne trouve pas que Pierre se trompe (ni Anne, en effet).
- 28 Nov 2012, 16:34
- Forum: ✎ Collège et Primaire
- Sujet: DM n°5 Niveau 3 ième - équations
- Réponses: 5
- Vues: 812
Oui, c'est un peut court, ta remarque, finonacci.
Car en plus d'être fausse, ta réponse me parait bien baroque, c'est à dire compliquée (comme la façade d'une cathédrale baroque mexicaine).
;-)
Car en plus d'être fausse, ta réponse me parait bien baroque, c'est à dire compliquée (comme la façade d'une cathédrale baroque mexicaine).
;-)
- 28 Nov 2012, 16:21
- Forum: ✎ Collège et Primaire
- Sujet: Problème de billes
- Réponses: 8
- Vues: 1432
Bonjour 444 ! Tu as déjà bien avancé, je vois... "Déterminer l'ensemble de définition" Dans ton exercice, x représente une distance en mètres, celle de la partie grillagée AB. Peut-on avoir des valeurs négatives de x ? comme x = - 3 ? Peut-on avoir des valeurs grandes de x ? comme x = 10 0...
- 28 Nov 2012, 16:14
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les équations
- Réponses: 9
- Vues: 1067
- 29 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
