Hmm...je bloques aidez moi svp.
128 résultats trouvés
Revenir à la recherche avancée
une preuve
Prouver que si  et
et 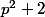 sont premiers, alors
sont premiers, alors 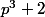 l'est aussi.
l'est aussi.
Hmm...je bloques aidez moi svp.
Hmm...je bloques aidez moi svp.
- 28 Sep 2015, 02:15
- Forum: ⚔ Défis et énigmes
- Sujet: une preuve
- Réponses: 13
- Vues: 678
SkilD a écrit:J'ai trouvé que h(x)-g(x)=x^3-3x+2
Donc que x^3-3x+2=0 et ensuite en calculant le discriminent on trouve 2racines réelles qui sont 1et-1 et là, le néant, je sais pas à quoi ça nous sert..
on trouve (3x^2 + 3)/(1+x^2), constante
- 04 Fév 2015, 21:43
- Forum: ✎✎ Lycée
- Sujet: Avec un peu d'astuce..
- Réponses: 5
- Vues: 610
théorème de pythagore
bon alors,
connaissez vous des preuves originales (et pas trop longues) du théorème de pythagore? on laisse les preuves classiques qu'on peut trouver facilement sur le wiki.
moi j'en connais une que j'aurais le plaisir de partager bientôt ^^
:zen:
connaissez vous des preuves originales (et pas trop longues) du théorème de pythagore? on laisse les preuves classiques qu'on peut trouver facilement sur le wiki.
moi j'en connais une que j'aurais le plaisir de partager bientôt ^^
:zen:
- 14 Déc 2014, 00:32
- Forum: ⚜ Salon Mathématique
- Sujet: théorème de pythagore
- Réponses: 0
- Vues: 557
Ben voilà, c'est ça le développement en série de Taylor de VA au voisinage de deux
Le mec qui t'a demandé ça, il voulait juste troller :lol3: Pour être plus explicite, le développement de Taylor à l'ordre n d'une fonction, c'est approximer cette fonction par un polynôme de degré n. Donc quand au v...
séries
Bon matin,
On m'a demandé de trouver la série de Taylor au voisinage de 2 pour la fonction valeur absolue...et je sais pas comment faire!! :mur: :cry: Au secours svp!
On m'a demandé de trouver la série de Taylor au voisinage de 2 pour la fonction valeur absolue...et je sais pas comment faire!! :mur: :cry: Au secours svp!
complexes
salut,
J'ai un exo qui me demande de résoudre l'équation suivante pour dans C
dans C
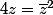
je cherche une solution simple (qui utilise une propriété des conjugués par exemple) plutôt que de remplacer z par a+bi. des idées?
J'ai un exo qui me demande de résoudre l'équation suivante pour
je cherche une solution simple (qui utilise une propriété des conjugués par exemple) plutôt que de remplacer z par a+bi. des idées?
salut, merci de vos réponses Le petit théorème permet d'écrire \ x^{p-1}\equ 1\ [p] et soit le plus petit entier positif d tel que \ x^{d}\equ 1\ [p] . En utilisant Bézout, on obtient \ x^{\text{pgcd}((p-1),d)}\equ 1\ [p]\ comme (p-1)>0 et d > 0 , on a 0 < pgcd(p-1,d)...
- 05 Nov 2014, 02:43
- Forum: ✎✎ Lycée
- Sujet: congruence
- Réponses: 5
- Vues: 384
congruence
Bonjour,
Soit un entier et un nombre premier
et un nombre premier  où
où  ne divise pas
ne divise pas  .
.
Prouvez que :
Si est le plus petit entier positif tel que
est le plus petit entier positif tel que  = 1) , alors
, alors
 divise
divise  .
.
Soit un entier
Prouvez que :
Si
- 04 Nov 2014, 08:21
- Forum: ✎✎ Lycée
- Sujet: congruence
- Réponses: 5
- Vues: 384
loulya a écrit:Merci pour votre réponse
Mais pourquoi les menteurs seraient Charles et André?? Parce que se sont eux qui accusent les autres?
André et Boris ne peuvent pas jamais être tous les deux menteurs, donc Charles doit être menteur. Alors Daniel est honnête, puis André est menteur...etc
- 19 Oct 2014, 15:56
- Forum: ✎✎ Lycée
- Sujet: Exercice de logique !!!
- Réponses: 5
- Vues: 656
- 19 Oct 2014, 14:57
- Forum: ✎✎ Lycée
- Sujet: Exercice de logique !!!
- Réponses: 5
- Vues: 656
- 19 Oct 2014, 14:45
- Forum: ✎✎ Lycée
- Sujet: équation diophantienne
- Réponses: 98
- Vues: 5822
ennaji00001 a écrit:salut tout le monde
s'il vous plait aider moi a resoudre cette exercice j'ai bien cherché mais rien trouvé
montrer que 1^3+2^3+3^3+4^3=(1+2+3+4)^2
merci d'avance
bah...vous calculez tout si vous êtes vraiment mal pris.
- 02 Oct 2014, 02:42
- Forum: ⚔ Défis et énigmes
- Sujet: demonstration
- Réponses: 3
- Vues: 980
avez-vous déjà essayé le jeûne? Sans le vouloir, j'ai jeûné la fin de semaine dernière et je peux vous dire que ça ne rend pas plus intelligent ni éveillé, même que ça procure tout l'effet contraire. Je prend quatre fois plus de temps à faire une même tâche que je n'en prenais avant de jeûner. J'ai ...
- 02 Oct 2014, 02:31
- Forum: ⚜ Salon Mathématique
- Sujet: devenir plus intelligent
- Réponses: 40
- Vues: 3983
donc, on suppose 13 divise 3^{n+2} + 4^{2n+1} soit 4^{2n+1}=13k-3^{n+2} On considère: 3^{n+3}+4^{2n+3}=27\times 3^n +16\times 4^{2n+1} Remplace 4^{2n+1} par 13k-3^{n+2} 3^{n+3} + 4^{2n+3} = 13(16k - 13\times 3^{n+2}) = 13m avec m entier. :zen: tiens, j'y avais pas pensé :hum:
- 30 Sep 2014, 22:58
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 9
- Vues: 596
Doraki a écrit:!??
Tu peux toujours réécrire 16^n en (13+3)^n puis développer, t'obtiens des tas de multiples de 13, puis un 3^n, que tu regroupes avec l'autre 3^n pour avoir 13*3^n.
merci, c'est fait.
mais il y a plus simple encore, comme on n'a pas encore vu le binôme de newton.
- 30 Sep 2014, 22:43
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 9
- Vues: 596
Doraki a écrit:3^(n+2) + 4^(2n+1) = 9*3^n + 4*16^n
Comme 16 est congru à 3 et que 9 est congru à -4, ....
salut,
on n'a pas encore vu les congruences, il y a une autre façon?
- 30 Sep 2014, 22:18
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 9
- Vues: 596
arithmétique
Bonjour,
Je n'arrive pas à résoudre cette exercice ; j'ai essayé par récurrence sur n:
Prouver que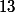 divise
divise 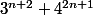 pour tout entier n
pour tout entier n
Je prouve le cas n=1, supposons le cas n=k
cas n= k+1: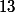 divise
divise 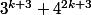
Je n'arrive pas à résoudre cette exercice ; j'ai essayé par récurrence sur n:
Prouver que
Je prouve le cas n=1, supposons le cas n=k
cas n= k+1:
- 30 Sep 2014, 21:48
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 9
- Vues: 596
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
