Forum de Mathématiques: Maths-Forum

Merci beaucoup !! Ca m'aide beaucoup !
Je partage votre sentiment quant à la réponse plus que succincte de cette élève.

Bonjour Je suis en M1, j'ai des cours de préparation à l'oral et voici ce que mon enseignant me propose de faire EXERCICE Thème : suites Soit f la fonction définie par : f(x) = ln(x) + x 1) Soit un entier naturel non nul, on s'intéresse à l'équation : (En) ln(x) + x = 1/n Justifier qu'elle admet une...

Bonsoir Le but est de montrer qu un espace de Banach uniformément convexe est réflexif. On prend u de E" de norme 1. Pour f \in E ' et \varepsilon > 0 , on appelle V_{f,\varepsilon} l'ensemble des éléments x de E, de norme inférieur ou egale à 1 tels que ||f(x) - u(f)|| <= \vare...

Concrètement je ne comprends pas à quoi ressemble mon morphisme

on a aussi Q(-x) = 0

Doraki a écrit:oui. P(-y) = 0, en envoyant y sur x+1, ça te dit que P(-x-1) = 0, et donc maintenant en prime tu connais les deux racines de P dans F3[X]/P : x et -x-1.
Q a aussi une autre racine à part x+1.

Je ne comprends pas ou vous voulez en venir

mirlamber a écrit:Oui moi aussi
j'ai aussi que P(-y) = 0

donc morphisme c'est

x -> -y
cela dit, on a plus dans ce cas, f(1) = 1 ?

remarque on s'en fou on impose que 1 -> 1, 0 -> 0 et 2 -> 2 et pour le reste on se base sur x -> -y ?

Oui moi aussi
j'ai aussi que P(-y) = 0

donc morphisme c'est

x -> -y
cela dit, on a plus dans ce cas, f(1) = 1 ?

Bon bah en fait je trouve pas

Ah non c'est faux mais j'ai compris pourquoi je vais corriger

j'ai trouvé que Q(x + 1) = 0

donc le morphisme qui envoye x sur y - 1 convient je pense ?

Doraki a écrit:Bah oui, Q(y)=0 alors que Q(x) = x.

Il faut chercher un élément z de F3[x]/P tel que Q(z)=0, et dire que tu envoies y sur z.

ooooh d'acc ! je ne l'avais pas vu comme ça, j'ai toujours du mal à manipuler les éléments des ensembles de type F3/(P)

je cherche le morphisme
Merci de vos explications

oui ça revient au même, c'est juste que là j'avais la flemme de dire que je faisais l'algorithme de division et j'ai tout de suite sorti le bon quotient. Je vois J'ai essayé de choisir le morphisme qui envoye x sur y, x + 1 sur y + 1 etc.. ça ne marche pas car on a pas si on note f le morphisme, f(...

J'ai juste changé de représentant dans la classe de x² dans F3[X]/P. La classe de x² dans F3[X]/P c'est l'ensemble des polynomes B tels que B-x² est multiple de P. x²-P est dedans parceque (x²-P)-x² = (-1)*P, qui est un multiple de P. Donc x² et x²-P sont dans la même classe d'équivalence : La clas...

Bonjour, une autre façon de voir les choses, moins rigoureuse que celle donnée par Doraki. L'ensemble K[X]/(P) peut se voir comme l'ensemble des objets que tu peux construire à partir des trois ingrédients suivants : - les éléments de K - un nouvel élément X qui satisfait P(X) = 0 - les opérations ...

oui pardon. Par contre il te manque -x, -x+1, et -x-1 dans tes représentants. Et non c'est pas la même chose parcequ'ils se multiplient pas de la même façon. Si tu prends la classe de x dans F3[x]/P, tu as cl(x)*cl(x) = cl(x*x) = cl(x²) = cl(x² - P) = cl(-x+1) Si tu prends la classe de y dans F3[y]...

Le polynome est plutot de degré strictement inférieur à 2 non ? puisque P est de degré 2

Dans ce cas je dirai que les éléments de F3/(P) s'écrivent donc
0, - 1, 1, x, x + 1 et x - 1 non ?

Q étant aussi de degré 2, alors les éléments de F3/(Q) c'est exactement les memes ?!

Justement mon probleme c'est que je n'arrive pas à écrire les éléments de F3/(P)
Est ce que vous pouvez me dire comment ils s'écrivent ?

Bonjour

Soit P = x² + x + 2 et Q = y² + 2y + 2

Ces 2 polynomes sont irréductibles

Je dois montrer que les corps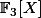 /(P) et /(Q) sont isomorphes en construisant un isomorphisme

Je n'ai pas trop d'idée
merci d'avance