17 résultats trouvés
Revenir à la recherche avancée
Une fois que tu as a et b tu les remplace dans les équations de tangente ? Et comment passes-tu de a=b-1 à -a+1=-b-1 Pour finir l'exercice j'ai fait comme ceci : On calcule l'image de points a et b A(1/2;exp(1/2)) B(-3/2;-exp(1/2)) Les points A et B appratiennent à une même doite de coeff dir exp(1...
- 09 Nov 2012, 11:57
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
(1): exp(a)=exp(-b-1) a=-b-1 on remplace exp(-b-1) par exp(a) dans : (2): -exp(a)a+exp(a)=-exp(-b-1)b-exp(-b-1) ça donne : -exp(a)a+exp(a)=-exp(a)b-exp(a) -a+1=-b-1 on remplace b par -a-1: -a+1=-b-1-a+1=a+1-1a=1/2 Une fois que tu as a et b tu les remplace dans les équations de tangente ? Et comment...
- 09 Nov 2012, 10:58
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:par bijectivité de lexponentielle, exp(a)=exp(-b-1) a=-b-1
remplace dans (2) pour résoudre le système dans son intégralité
je trouve
b=exp(-b-1)-1
a=-exp(-b-1)
est ce correcte
- 09 Nov 2012, 01:58
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:très bien
que donne exp(a)=exp(-b-1)?
J'arrive pas à isoler dans la 2 eme égalité exp (a) pour pouvoir remplacer dans la première et ensuite avoir que b comme inconnu
- 09 Nov 2012, 01:17
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
[quote="bentaarito"]Pourquoi exp(a)=-exp(-b-1) ?
c'est quoi l'ordonnée à l origine de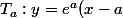+e^a) [/
[/
:mur: je me suis trompé j'ai pas les bonnes ordonnées à l'origine
Après corrections on a
exp(a)=exp(-b-1)
-exp(a)*a+exp(a)=-exp(-b-1)*b-exp(-b-1)
c'est quoi l'ordonnée à l origine de
:mur: je me suis trompé j'ai pas les bonnes ordonnées à l'origine
Après corrections on a
exp(a)=exp(-b-1)
-exp(a)*a+exp(a)=-exp(-b-1)*b-exp(-b-1)
- 09 Nov 2012, 01:01
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:tu appliques ça pour tes tangentes
t es censé trouver le resultat donné par chan97
Donc on a
exp(a)=exp(-b-1)
exp(a)=-exp(-b-1)
exp(-b-1)=-exp(-b-1) ---> on trouve b
et après on se sert des équations du dessus
- 09 Nov 2012, 00:28
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:il faut qu il ait mm coef dir -->a1=a2
et un point en commun --> b1=b2
OK merci ! Mais après avec ces deux égalité ont fais quoi ?
- 08 Nov 2012, 23:33
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:si
comment traduire D1=D2 ?
Je vois pas comment ecrire ça avec les équations je sais qu'elles ont le meme coeff et au moins un point en commun mais je sais pas ou plus l'écrire avec les équations
- 08 Nov 2012, 23:26
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:attention! c'est pas les bons coef dir! j'ai corrigé dans mon post
et non pour la 2eme! on égalise pas les images des points comme ça
je vois pas trop ce que tu veux dire
- 08 Nov 2012, 23:13
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:je comprends pas ton système
la première égalité correspond aux deux coefficient directeur des tangentes Ta et Tb
la deuxième égalité correspond aux deux points qui doivent être égaux
- 08 Nov 2012, 23:07
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:Non!
deux droites sont égales ( confondues ) si elle s ont même coef directeur et qu'elles ont un point commun
C'est là qu'intervient le système
Il faut que :
exp(a)=-exp(-b-1)
exp(a)=exp(-b-1)
- 08 Nov 2012, 22:59
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
bentaarito a écrit:et comment comptes tu résoudre ça?
On remplace par les expressions trouvées
exp(a)*(x-a) + exp(a) = - exp(-b-1) (x-b) + exp(-b-1)
exp(a)*x-exp(a)*a + exp(a) = - exp (-b-1)*x - exp(-b-1)*-b + exp(-b-1)
exp(a)*(x-a+1)=exp(-b-1)*(-x+b+1)
Mais après :mur:
- 08 Nov 2012, 22:38
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
chan79 a écrit:Slt
Tu peux montrer que les coubes C et C' sont symétriques par rapport au point (-1/2,0)
Comment fais-tu pour montrer que deux courbe sont symétriques ?
- 08 Nov 2012, 22:07
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
faux! déjà pour être rigoureux , ça ce n'est en rien une équation, c'est juste une formule qui veut pas dire grand chose tu dois écrire : T_a: y =e^a(x-a)+e^a et pour la deuxième T_b: y =-e^{-b-1}a(x-a)+e^{-b-1} J'ai choisi a et b qui sont pas forcement égaux !raison de plus que les...
- 08 Nov 2012, 22:04
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
- 08 Nov 2012, 21:28
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
- 08 Nov 2012, 21:12
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
Tangente commune et exponentielle
Bonjour, J'ai un problème ouvert à faire pour jeudi prochain mais je n'y arrive pas. J'ai déjà fais la figure sur un logiciel de géométrie et j'ai conjecturer qu'il en existe une. Mais je n'arrive pas à le démontrer. Voici l'énoncé : Existe-t-il une (des) tangente(s) commune(s) aux courbes C et C' d...
- 08 Nov 2012, 20:52
- Forum: ✎✎ Lycée
- Sujet: Tangente commune et exponentielle
- Réponses: 36
- Vues: 6476
- 17 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
