Forum de Mathématiques: Maths-Forum

Zapotek a écrit:J est un segment donc compact. De plus f est continue sur J...ça ne te rappelle pas un résultat?

non .je suis bete :mur:

soient I et J deux intervalles et (g_n) une suite de fonctions de I dans J qui converge uniformément sur I ver une foinction g .soit f\inC^0(J,\mathbb{R}) et (h_n) la suite définie pa h_n=fog_n . 1.Montrer que si J est un segment, alors la suite (h_n) converge uniform...

ptitnoir a écrit:Oui................................

mais pour la troisiéme cas y'a deux cas qui se pose tend vers L ou l'infini

arnaud32 a écrit:en effet c'est bien ce que ca prouve: tu ne peux rien conclure quand a la convergence de la serie des vn si celle des un diverge

mais si la limite de tend vers 0 ou l la serie de terme general diverge grossierement

@oudbib Je pense qu'on peut supposer que le terme u_n tend vers 0 quand n tend vers +infini ( sinon la série \bigsum_{k=0}^{\infty}u_n divergerait "grossièrement" ) ET à priori on ne sait pas ce qu'est la limite du terme n^2u_n quand n tend vers +infini donc : Pourquoi dis tu cela ? effec...

@oudbib je pense que quand tu dis diverge cela veut dire que \bigsum_{k=0}^{\infty} u_n= + \infty ? Conseil : étudie les 3 cas 1) limite de n^2 u_n quand n tend vers +infini tend vers +infini 2) limite de n^2 u_n quand n tend vers +infini tend vers une limite L 3) limite de n^2 u_n quand n tend ver...

@oudbib je pense que quand tu dis diverge cela veut dire que \bigsum_{k=0}^{\infty} u_n= + \infty ? Conseil : étudie les 3 cas 1) limite de n^2 u_n quand n tend vers +infini tend vers +infini 2) limite de n^2 u_n quand n tend vers +infini tend vers une limite L 3) limite de n^2 u_n quand n tend ver...

soit une suite réelle positive et
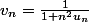
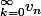
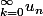
etudier le cas ou diverge

arnaud32 a écrit:ne peux tu pas voir les s_n comme une subdivision de R+?

merci de ton aide :lol3:

arnaud32 a écrit:est ce que par hasard la serie des u_n ne serait pas a termes positifs?

oui exactement elle est a termes positifs :mur:

Nightmare a écrit:La différence est que la première a une valeur de vérité, contrairement à la deuxième.

:lol3:

.la série de terme général converge.
je suis désole :mur:

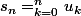
on suppose que la série à termes général est divergente et on pose soit une application de à continue et décroissante.comparer les énoncés:
1. est intégrable
2.la série de terme général converge