19 résultats trouvés
Revenir à la recherche avancée
Trouver une équation différentielle
Bonjour, Je suis en train de faire un numéro sur les équations différentielles et je n'arrive pas à tomber sur la bonne réponse qui est donnée à la fin du corrigée. D'abord, faut dire que j'ai toujours eu un peu peur des éq. différentielles, alors c'est une des raisons pour laquelle je sollicite de ...
- 01 Oct 2012, 19:10
- Forum: ✎✎ Lycée
- Sujet: Trouver une équation différentielle
- Réponses: 0
- Vues: 448
- 27 Sep 2012, 01:58
- Forum: ✎✎ Lycée
- Sujet: Racines d'un polynôme complexe
- Réponses: 10
- Vues: 756
Est-ce que c'est une méthode fiable qui fonctionne relativement bien pour les racines du type 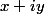 ? Ou bien, elle fonctionne dans cette situation ci, mais il pourrait arriver qu'elle ne fonctionne pas ? Parce qu'on impose un peu le
? Ou bien, elle fonctionne dans cette situation ci, mais il pourrait arriver qu'elle ne fonctionne pas ? Parce qu'on impose un peu le  non ? ..
non ? ..
- 27 Sep 2012, 01:43
- Forum: ✎✎ Lycée
- Sujet: Racines d'un polynôme complexe
- Réponses: 10
- Vues: 756
Tu sais que tu as entièrement raison haha. En y pensant comme il faut, le problème est assez facile, seulement j'avais pas compris pourquoi eux ils arrivaient toujours avec les 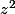 , mais je me rend compte que c'est simplement en multipliant les facteurs semblables !!
, mais je me rend compte que c'est simplement en multipliant les facteurs semblables !! 
Merci sérieusement !!
Merci sérieusement !!
- 27 Sep 2012, 01:29
- Forum: ✎✎ Lycée
- Sujet: Racines d'un polynôme complexe
- Réponses: 10
- Vues: 756
Donc, pour le  , comment est-ce que j'entreprend mes démarches puisque j'ai déjà éclairci pour
, comment est-ce que j'entreprend mes démarches puisque j'ai déjà éclairci pour  .
.
J'ai donc besoin d'une ( ) qui est nulle lorsque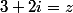 ?
?
J'ai donc besoin d'une ( ) qui est nulle lorsque
- 27 Sep 2012, 01:21
- Forum: ✎✎ Lycée
- Sujet: Racines d'un polynôme complexe
- Réponses: 10
- Vues: 756
La seule à laquelle je peux penser rapidement est que
Si est une racine de P, alors son conjugé en sera une également . P(w) = 0.
est une racine de P, alors son conjugé en sera une également . P(w) = 0.
Mais je ne crois pas que c'est à ce que vous faites allusion cependant, est-ce que je me trompe ? :help:
Si
Mais je ne crois pas que c'est à ce que vous faites allusion cependant, est-ce que je me trompe ? :help:
- 27 Sep 2012, 01:14
- Forum: ✎✎ Lycée
- Sujet: Racines d'un polynôme complexe
- Réponses: 10
- Vues: 756
Racines d'un polynôme complexe
Bonjour, Voilà, j'ai un problème qui me demande de trouver un polynôme à coefficients réels qui possède les racines : [CENTER] \sqrt{3} , -\sqrt{3} , i , 3 + 2i [/CENTER] Bon, j'arrive à trouver pour les 2 racines et le i : [CENTER] P(z) = (z^2 + 3)(z^2 + 1) [/CENTER] Mais, e...
- 27 Sep 2012, 01:02
- Forum: ✎✎ Lycée
- Sujet: Racines d'un polynôme complexe
- Réponses: 10
- Vues: 756
Donc, si je saisie moindrement après un peu de temps de réflexion : z^4 = 1 Donc; (re^{i\theta})^4 = 1*e^{i(0 + 2k\pi/2)} 0 ici à cause que 1 = cos 0 + isin0, vrai? r^4e^{4i\theta} = 1*e^{i(0 + 2k\pi/2)} r^4 = 1 4i\theta = 0 + 2k\pi/2 De là, r = 1 \theta = 2k\pi/8 = k\pi/4 Do...
- 26 Sep 2012, 22:19
- Forum: ✎✎ Lycée
- Sujet: Résoudre Polynôme complexe
- Réponses: 6
- Vues: 518
Luc a écrit:Ok.
Et, tu saurais résoudre?
Non, je suis embêté je dois avouer. . . d'où mon besoin de comprendre un peu la méthode de résolution.
- 26 Sep 2012, 21:07
- Forum: ✎✎ Lycée
- Sujet: Résoudre Polynôme complexe
- Réponses: 6
- Vues: 518
Évidemment que z = 3 C'est à partir de ce point que je ne sais plus comment m'y prendre. J'ai toujours de la difficulté dès que l'on dépasse le bornes -1 .. +1 du cercle trigo pour trouver les angles. Alors j'imagine que c'est plus simple d'écrire dans ce cas quelque chose comme z = +ou- (3 + 3i...
- 26 Sep 2012, 20:52
- Forum: ✎✎ Lycée
- Sujet: Résoudre Polynôme complexe
- Réponses: 6
- Vues: 518
Résoudre Polynôme complexe
Bonjour, Je suis à un numéro qui demande d'abord d'écrire en facteurs linéaires ou quadratiques irréductibles réels et également de donner les racines de l'expression suivante: z^4 - 81 Bon, du coup, j'arrive à comprendre que je peux commencer par faire z^4 = 81 (x+iy)^4 = 81 ? Mais par la s...
- 26 Sep 2012, 20:43
- Forum: ✎✎ Lycée
- Sujet: Résoudre Polynôme complexe
- Réponses: 6
- Vues: 518
- 26 Sep 2012, 19:00
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
Rebonjour, J'ai frappé un deuxième obstacle concernant les nombres exponentiels complexes. Voilà, je dois trouver tous les nombres z tel que e^{iz^2}=e^{-z} Et j'ai vraiment de la difficulté à débuter le problème, je ne sais pas par où commencer mon analyse, je ne veux pas une réponse complète, mais...
- 26 Sep 2012, 18:51
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
Haha, merci pour la réponse, pendant que tu as écrit ta réponse, j'étais au même moment en train d'écrire ma réponse!!! :we: !!
- 26 Sep 2012, 17:49
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
Ahhhhhh ! Je viens de réaliser je crois !! Puisque la deuxième portion, soit http://www.maths-forum.com/images/latex/e824c645275162ab366d283a61748bec.gif alors il reste e^( http://www.maths-forum.com/images/latex/42affa250aeca5ce9ddd99787cfc0ebb.gif * http://www.maths-forum.com/images/latex/865c0c0b...
- 26 Sep 2012, 17:48
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
Merci pour la réponse, Je comprend très bien http://www.maths-forum.com/images/latex/e824c645275162ab366d283a61748bec.gif pour la simple raison que le cos( http://www.maths-forum.com/images/latex/42affa250aeca5ce9ddd99787cfc0ebb.gif ) + http://www.maths-forum.com/images/latex/865c0c0b4ab0e063e5caa33...
- 26 Sep 2012, 17:46
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
En fait, la question est simplement : Écrire la forme cartésienne du nombre complexe http://i48.tinypic.com/22hi.png Et la réponse est supposé être = i . Il n'y a rien de plus.. Le e^i(pi/2) selon moi sera égale simplement à : cos(pi/2) + i*sin(pi/2) Mais là où j'ai un problème à comprendre, c'est l...
- 26 Sep 2012, 17:37
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
annick a écrit:Bonjour,
tu parles de résultat, mais on ne sait pas d'où tu es parti.
Désolé, ce n'était pas claire, le résultat attendu en fait est :
Le problème ci-haut, est le point de départ !! Désolé pour la confusion
- 26 Sep 2012, 17:22
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
Calcul exponentiel complexe grrr
Bonjour, D'abord, je suis nouveau ici, je suis présentement à l'Université en médecine. J'ai un cours complémentaire en calculs etc. . . Bref, nous sommes à voir les nombres complexes. Il y a un numéro qui membête drôlement, et malgré l'utilisation de l'application WolfCalc, je n'arrive pas à compr...
- 26 Sep 2012, 17:18
- Forum: ✎✎ Lycée
- Sujet: Calcul exponentiel complexe grrr
- Réponses: 13
- Vues: 838
- 19 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
