Forum de Mathématiques: Maths-Forum

Arnaud-29-31 a écrit:Bein fais le tu verras que oui.

J'arrive pas á tomber net sur (x³-12x-18)/(3x³)
je suis tombé sur x³+20x²+30x/3x³

Non ... On avait (\frac{x^3-6x^2+12x+9}{x^2})' = \frac{(3x^2-12x+12)x^2-(x^3-6x^2+12x+9)(2x)}{x^2} une fois les parenthèses ajoutées. Il faut simplement développer le haut de la fraction .... okay donc en développant le haut de la fraction, sa donne x³-12x-18/3x³ ?

Je ne comprends vraiment pas ce que tu fais ... j'ai l'impression que des additions se sont transformée en multiplications. Quand tu fais un développement il faut bien écrire les choses pour ne pas oublié de facteur, mais dans ton post précédant tu as oublié les parenthèses d'où peut être une des e...

Arnaud-29-31 a écrit:Oui, à part le -(-12x) pourquoi deux signes - ?

Il faut maintenant développer puis simplifier et on arrive au résultat.

Ah ouais c'est une faute de frappe, je voulais écrire (-12x)

okay alors développement :
[-36x² +12x² ] - [x³-6x²+22x] / 2x²
= (x³-6x²-18 ) / (x³)

J'ai l'impression que tu ne maitrises pas ce dont on parle. On ne calcule pas u et v. L'écriture (\frac{u}{v})' = \frac{u'v-uv'}{v^2} montre simplement comme dériver un quotient. On peux donc poser u = le haut de la fraction et v = le bas de la fraction pour ensuite dériver ces ...

Arnaud-29-31 a écrit:?!

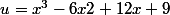
Ici et

Ah d'accord merci.
Et donc une fois que jai calculé u/v , je dois faire quoi pour montrer que pour tout réel x de [1;10] on a f'(x) = (x³-12x-18) /(x³)

Arnaud-29-31 a écrit:Donc si on utilise la formule , c'est quoi et c'est quoi ?

u c'est x³-6x²
v c'est 12x+9

Arnaud-29-31 a écrit:Je ne comprend pas comme tu choisis u et v.

La fonction est bien ??

Oui c'est la fonction.

Arnaud-29-31 a écrit:As tu dérivé la fonction en utilisant la formule de dérivée d'un quotient ?

Oui j'ai écris : u/v = u'v-v'u / v²
u = x³-6x² ; v=12x+9
u'=3x²-12x v=12 + 0, donc 12

L'énoncé ne peut pas que être ça, ce n'est pas complet ... Oui il n'y a pas de parenthèse dans ton bouquin mais sur le forum tu écris en ligne, il faut donc lever le doute. f(x) = \frac{x^3-12x-18}{x^3^} ou f(x) = x^3-12x-\frac{18}{x^3} ce n'est pas la même chose ... Okay , euh oui ...

Bonsoir, Ton énoncé n'est pas clair. Quelle est la question ? Et comment est définie f ? Tu ne mets pas de parenthèse c'est donc dur de deviner. Dans tout les cas ta dérivée n'a pas l'air juste. La question est : Montrer que pour tout réel x de [1;10] , on a : f(x) = x ³- 12x-18 / x ³, dans mon man...

Bonjour jai fait un exercice mais je sais pas si c'est juste . Est-ce que vous pouvez me dire si ce que j'ai fait est juste? L'énoncé c'est : Montrer que pour tout réel x de [1;10] , on a : f(x) = x ³(au cube) - 12x-18 / x ³ (au cube) J'ai fait la dérivée de f(x) = 3x² -12 / 3x² = 9x² -12 / 3x² merc...