Forum de Mathématiques: Maths-Forum

Merci à tous pour votre aide! :happy2:

si je l'ai bien vu, c'est rebarbatif à faire car c'est toujours les même calculs...

Merci,
après l'avoir fait pour Z0, Z1 et Z2 j'ai remarqué que pour chaque solutions z trouvées, en posant z=x+iy, on a x²=y². C'est bon?

ps: une page de développement par solution Z :hum: je vais éssayer de comprendre ton idée de départ, à savoir factoriser.

ok j'ai enfin trouvée la simplification :happy2:

Pour Z1, on trouve z^2 = \frac{e^{\frac{2i\pi}{8}} + 1}{e^{\frac{2i\pi}{8}} -1} = \frac{ e^{\frac{i\pi}{8}} + e^{-\frac{i\pi}{8}}}{ e^{\frac{i\pi}{8}} - e^{-\frac{i\pi}{8}} } = \frac{\cos{\frac{\pi}{8}}}{i \sin{\frac{\pi}{8}} } = e^{-\frac{i\pi}{2}} \frac{\cos{\frac{\pi}{8}}}{ \sin{\frac{\pi}{8}} }...

Quelqu'un saurait il m'aider svp?

Quand je le fais pour Z0, je ne trouve aucune solution. Quand je le fais pour Z1, je trouve Z1=(1-\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2})z^2 + (1+\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2})=0 et j'en déduis des valeurs invraissemblables du genre x^2=\sqrt(\frac{\sqrt{80+24\sqrt{2}}}{...

Oula effectivement j'enchaine les erreurs. Je reprends, les 8 racines huitième de 1 sont de la forme : Zk=e^i(\frac{2k\Pi}{8}) donc par exemple pour k=0 on a Z0=1 . Dois-je en déduire que les deux premières solutions de l'équation de départ vérifient \frac{z^2+1}{z^2-1} =1 ??? car si oui j'e...

Je sais seulement que les 8 solutions sont de la forme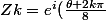 avec
(edit: j'avais fais une erreur)

ensuite pour par exemple,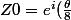
j'en déduis que ?

Si je pose Z= \frac {z^2+1}{z^2-1} , pour trouver le module de Z dois-je remplacer Z par (x+iy) ? puis ensuite simplifier Z , et trouver son argument? abcd22 merci mais je ne comprends pas trop ta méthode et je suis censé le résoudre avec des notions déjà vues en cours ou en TD. Cela ne me d...

je ne comprend pas très bien ta méthode abcd22

Ok donc si j'ai bien compris il y a au maximum 16 solutions, et ce n'est pas très compliqué, c'est surtout long à faire! Je vais commencer ce soir alors :mur:

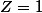Si je pose alors l'équation admet 8 solutions qui sont les 8 racines huitième de 1 c'est bien ça? Si oui que dois-je ensuite faire?

Bonjour!
le professeur nous a dit que l'équation suivante était longue à résoudre. Je voudrait que vous me donniez des pistes.

[(z²+1)/(z²-1)]^8 = 1

merci