Forum de Mathématiques: Maths-Forum

MacManus a écrit:Au final, on a majoré par 2*(1/2n)

Je te remercie beaucoup j'ai tout compris !

Lui même inferieur à 1/n

MacManus a écrit:C'est vrai, mais pour le coup, je dirai que c'est trop grossier
pour tout entier naturel n , on a 2n < 2n+1 donc .... ??

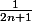
donc, (pour tout n de N*, cf mon edit)

Ce que tu écris n'est pas faux en soi, mais on te demande de majorer la valeur absolue. J'ai juste utilisé la propriété de l'inégalité triangulaire : \forall x,y \in \mathbb{R}^2 , |x+y| \le |x| + |y| \forall n \in \mathbb{N} \quad |2n+1| = 2n+1 et par quoi peut-on majorer \frac{1}{2n+1} ? Je pense...

Bonjour, On a l'inégalité suivante : \left | sin(n) + (-1)^n cos(n) \right | \quad \le \quad \left|sin(n) \right | + \left |(-1)^n cos(n) \right | \quad = \quad \left | sin(n) \right | + \left |(-1)^n \right | \left | cos(n) \r...

Bonjour, afin d'obtenir cette inégalité, par quoi aimerais-tu majorer |sin(n) + (-1)^n cos(n)| ? J'ai pensé tout d'abord à dire que : sin(n) \le 1 puis que cos(n) \le 1 ensuite (-1)^n \le 1 enfin (-1)^{n}cos(n) \le 1 donc que sin(n)+(-1)^{n}co...

Bonjour, afin de bosser un peu pendant les vacances pour ne pas perdre le fil, je fais des exos de maths, or une question me pose un peu problème : \left| \frac{sin(n)+(-1)^ncos(n)}{2n+1} \right| \le \frac{1}{n} Si quelqu'un pouvait me lancer là dessus !! :we: Merci à tous :h...