En gros cette fonction f est la somme des 20 premiers termes de la suite géométrique définie par
4 résultats trouvés
Revenir à la recherche avancée
Je te remercie pour m'avoir éclairé
En gros cette fonction f est la somme des 20 premiers termes de la suite géométrique définie par et
et 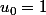
En gros cette fonction f est la somme des 20 premiers termes de la suite géométrique définie par
- 06 Aoû 2012, 14:11
- Forum: ✯✎ Supérieur
- Sujet: Somme d'exponentielles
- Réponses: 7
- Vues: 11884
Ok, je t'ai mis une petite variante si ça te tente. =) Merci :) Je vais m'amuser à le faire après Simplement, l'énoncé "simplifier suivant les valeurs de x", ça veut dire "réduire un maximum après avoir transformé en formule de sommation" ?? En gros la réponse c'est : \frac{1-e^...
- 06 Aoû 2012, 14:02
- Forum: ✯✎ Supérieur
- Sujet: Somme d'exponentielles
- Réponses: 7
- Vues: 11884
Attention, ce n'est pas une somme arithmétique mais une somme géométrique de raison e^x. :lol3: Non j'ai pas de problème à la calculatrice :p , mais comme tu as pu le voir j'ai edit mon post en rajoutant (mais je pense pas que ce soit valable avec l'exponentielle justement !!!) et j'ai trouvé tout ...
- 06 Aoû 2012, 13:55
- Forum: ✯✎ Supérieur
- Sujet: Somme d'exponentielles
- Réponses: 7
- Vues: 11884
Somme d'exponentielles
Bonjour, j'ai planché sur un énoncé mais vraiment je n'y arrive pas, j'ai seulement quelques pistes. D'abord voici l'énoncé : Simplifier suivant les valeurs de x f(x)=1+e^x+e^{2x}+...+e^{20x} Il est évident que c'est la somme des exponentielles de e^{0x} à e^{20x} J'ai donc fait la formule d...
- 06 Aoû 2012, 13:39
- Forum: ✯✎ Supérieur
- Sujet: Somme d'exponentielles
- Réponses: 7
- Vues: 11884
- 4 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
