56 résultats trouvés
Revenir à la recherche avancée
Equadiff d'ordre 2
Bonjour, J'ai une équation différentielle d'ordre 2 à résoudre mais je ne sais pas comment faire... La voici (c'est le résultat d'une superposition): (E2): y"-2y'+y=exp(x)+lnx On ne peut pas appliquer le théorème de superposition car les coefficients sont constants, alors comment fa...
- 23 Sep 2012, 15:41
- Forum: ✯✎ Supérieur
- Sujet: Equadiff d'ordre 2
- Réponses: 1
- Vues: 504
Ah! Pardon ! Oui, faut que j'ouvre mieux les yeux ! :doh: Mais, j'ai un doute, si on a \lim_{x\to+\infty}\;\;{g(x)}=-1 alors , que peut-on dire de \lim_{x\to+\infty}\;\;{x.g(x)} ? Par ailleurs, l'avantage de faire attention au signe de x, au lieu de prendre la valeur absolue (qui a ...
- 10 Aoû 2012, 17:02
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
- 10 Aoû 2012, 16:36
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
\lim_{x \to +\infty} sqrt{x^2+1}-2x+1 sqrt{x^2+1} = \sqrt{x^2(1+\frac{1}{x^2})} = |x|sqrt{1+\frac{1}{x^2}}-2x+1 avec x\neq0 |x|(sqrt{1+\frac{1}{x^2}}-2)+1 \lim_{x \to +\infty} sqrt{1+\frac{1}{x^2}}-2 = -1 \lim_{x \to +\infty} x(sqrt{1+\frac{1}{x^2}}-2)+1 = -\infty Je pense q...
- 10 Aoû 2012, 16:23
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
Non je n'ai pas oublier le x, je pense que tu ne l'as pas vu car j'ai du le mettre trop proche de la limite, sinon, oui je vois pourquoi x doit être différent de 0 :lol3: \lim_{x \to +\infty} sqrt{x^2+1}-2x+1 sqrt{x^2+1} = \sqrt{x^2(1+\frac{1}{x^2})} = |x|sqrt{1+\frac{1}{x^2}}-2x+1 avec x\ne...
- 10 Aoû 2012, 16:02
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
- 10 Aoû 2012, 15:13
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
- 10 Aoû 2012, 14:44
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
Problème sur une limite basique
Bonjour, J'ai un problème sur le calcul d'une limite. Je sais que la règle est qu'en + ou - \infty on prend le terme de plus haut degré. Mais dans l'exercice suivant, je ne sais pas quoi faire. \lim_{x \to +\infty} sqrt{x^2+1}-2x+1 \lim_{x \to +\infty} x^2+1 = +\infty \lim_{x \to +\infty} sqrt{x^2+1...
- 10 Aoû 2012, 11:21
- Forum: ✎✎ Lycée
- Sujet: Problème sur une limite basique
- Réponses: 20
- Vues: 1166
- 09 Aoû 2012, 14:45
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
Ah mais oui :-) Merci !! Du coups voici ENFIN la réponse : \sum_{k=1}^n \binom{n}{k} 3^{k-1} = \sum_{k=0}^n \binom{n}{k} 3^{k-1} - \binom{n}{0} 3^{0-1} \sum_{k=1}^n \binom{n}{k} 3^{k-1} = \frac{1}{3} \sum_{k=0}^n \binom{n}{k} 3^k - \frac{1}{3} \sum_{k=1}^n \binom{n}{k} 3^{k-1} = \frac{1}{3}(1+3&...
- 09 Aoû 2012, 14:22
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
- 09 Aoû 2012, 14:17
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
- 09 Aoû 2012, 14:11
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
- 09 Aoû 2012, 14:09
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
\binom40 = C_4^0 = \frac{4!}{0!4!} = 1 Je ne sais pas, moi ceci je l'admets... Bref là n'est pas le souci. Ah oui, désolé je n'avais pas vu cette erreur... Du coups ça donne ça donne ça : \sum_{k=1}^n \binom{n}{k} 3^{k-1} = \sum_{k=0}^n \binom{n}{k} 3^{k-1} - \binom{n}{0} 3^{0-1} \sum_{k=1}^n \bino...
- 09 Aoû 2012, 13:55
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
Je vais prendre le calcul, merci en tous cas ! Je vais peut-être réussir à éliminer toutes mes lacunes cet été. Donc pour revenir à mon calcul, ça donne bien ça : \sum_{k=1}^n \binom{n}{k} 3^{k-1} = \sum_{k=0}^n \binom{n}{k} 3^{k-1} - \binom{n}{0} 3^{k-1} \sum_{k=1}^n \binom{n}{k} 3^{k-1} = (1+3...
- 09 Aoû 2012, 11:44
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
Mais ça tu le vois avec les factoriels ?
!})
Il n'y a pas un moyen plus rapide car le temps de faire le calcul tu perds du temps.
Il n'y a pas un moyen plus rapide car le temps de faire le calcul tu perds du temps.
- 09 Aoû 2012, 11:10
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
S(n)=\sum_{k=1}^n \binom{n}{k} 3^{k-1} S(4)=\sum_{k=1}^4 \binom{4}{k} 3^{k-1} S(4)=\binom{4}{1} 3^0 +\binom{4}{2} 3^1 + \binom{4}{3} 3^2 + \binom{4}{4} 3^3 Jusqu'ici je suis tout à fait d'accord. Mais arrivé là ça se complique. S(4)= 4 \times 1 + 6 \times 3 + 4 \time...
- 09 Aoû 2012, 10:35
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
En fait c'est que j'ai déjà eu mon BAC, mais je n'ai malheureusement pas fait de BAC S, et je sais que les SOMMES et PRODUITS sont du programme de S, c'est pour cela que je poste dans la section lycée.
Mais je t'avoue que le détail de ton calcul me perd totalement.
Mais je t'avoue que le détail de ton calcul me perd totalement.
- 09 Aoû 2012, 10:08
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
Je vais prendre le calcul, merci en tous cas ! Je vais peut-être réussir à éliminer toutes mes lacunes cet été. Donc pour revenir à mon calcul, ça donne bien ça : \sum_{k=1}^n \binom{n}{k} 3^{k-1} = \sum_{k=0}^n \binom{n}{k} 3^{k-1} - \binom{n}{0} 3^{k-1} \sum_{k=1}^n \binom{n}{k} 3^{k-1} = (1+3...
- 08 Aoû 2012, 21:57
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
Ok, je vois, merci beaucoup
Donc si n vaut 3, avec k = 0, on a :
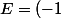^3+(-1)^2+(-1)^2+(-1)+1)
Ça donne ça en application numérique ?
Donc si n vaut 3, avec k = 0, on a :
Ça donne ça en application numérique ?
- 08 Aoû 2012, 21:14
- Forum: ✎✎ Lycée
- Sujet: Binome de Newton
- Réponses: 29
- Vues: 2142
- 56 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
