Forum de Mathématiques: Maths-Forum

Bonjour,

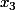est de signe quelconque, tu peux l'écrire : avec et

Une variable libre est remplacée par deux variables positives.

Est-ce que quelqu'un connait une méthode pour calculer cette intégrale ? \int_{-1}^{1} e^{\frac{1}{x^2-1}} dx [EDIT]Nan mais après ça coince de toute façon :hum: Je n'ai pas fait le calcul jusqu'au bout ... Mais par changement de variables j'arrive à : \int_0^1 e^{\frac{1}{x^2-1}} dx\quad =\quad \i...

tu a oublier le 2 2-\frac{2n+3}{2n}+\frac{2(n+1)-1}{2^{n+1}}=2+\frac{-4n-6+2n+1}{2^{n+1}} tu peux m'explique par étape comment en fait stp ^^ je n'ai pas mis le 2 parce qu'il n'a pas d'intérêt pour la question que tu poses à savoir "ramener deux fractions au même dénominateur" J'a...

D'accord, justement le truc c'est que je sais jamais si le neutre c'est 1, parce que pour moi la loi . pourrait très bien être l'addition et donc à ce moment là le neutre serait 0. Pourquoi est-ce que ce n'est pas possible que ce soit l'addition? En fait tu dois vraiment considérer que les lois * e...

[EDIT]Désolé j'avais pas compris ça comme ça.

Oui.

Je suppose que dans ton cas il est précisé que n = 2 ou bien que ton sous-espace vectoriel est de dimension 2 dans ?

Bonjour, C'est ça que tu as écrit : - \frac{2n+3}{2n}+\frac{2(n+1)-1}{2^{n+1}}=\frac{-4n-6+2n+1}{2^{n+1}} Oui c'est faux ! ça donne : - \frac{2n+3}{2n}+\frac{2(n+1)-1}{2^{n+1}}=\frac{-2(2n+3)}{2^{n+1}}+\frac{2(n+1)-1}{2^{n+1}}=\frac{-4n-6+2(n+1)-1}{2^{n+1}} et...

T'es sûr qu'il ne te manque pas des données dans ton exercice ?

Genre le pourcentage de chemisiers ayant un bouton manquant ?
Parce que là je ne vois pas bien comment faire ...

Déjà tu t'es planté dans la formule que j'ai écrit :!: Ensuite essaie d'écrire la formule qu'on t'a conseillé d'utiliser avec p = n - 2, simplifie un peu cette formule et tu devrais voir des choses apparaître entre cette formule et la formule astuce que je t'ai donnée ... Là je dirais que tu as tout...

Tu utilises cette petite formule pour te "débarrasser" du k², ensuite tu dois retrouver la formule qu'on te demande d'utiliser (celle pour p = n-2) mais il y a quelques manipulations à faire sur tes sommes.

Je ne t'ai pas écrit l'astuce complète pour que tu cherches parce que vous l'avez peut-être déjà vu en cours ou en exos.

C'est ça la formule à utiliser : k² = k(k-1) + k

Ah si je viens de trouver comment faire avec ta méthode ... mais il te faudra quand même la petite formule astuce dont je parlais. Bah commence par écrire la formule qu'on te dit d'utiliser avec p = n - 2, ensuite elle se simplifie un peu de façon à obtenir une formule qui ressemble aux formules que...

Pour moi non plus ça ne sert à rien mais dans la consigne il est écrit qu'il faut l'aplliquer en remplaçant p par n-2... Ok je vais chercher en utilisant cette formule alors. je ne sais pas si c'est à cette formule que tu fais réfèrence mais je pensais à somme de k allant de 0 à n = (n(n+1))/2 Non ...

Si x était un nombre, le produit Ax donnerait une matrice 3x3, or B est un vecteur 3x1, donc tu n'as pas le choix : X est un vecteur 3x1

X = (x, y, z), tu dois exprimer x, y et z en fonction de a, b, c et m.

Par contre après je dois calculer Somme de k allant de 0 à n k puissance 2 .comb(n,k) en me servant de la réponse précédente (le calcul de cette somme ou k n'est juste pas au carré) et d'une formule auparavant démontrée qui est la suivante: somme k allant de 0 à p comb(n,k)comb(n-k,p-k)= 2puissance...

c'est pas grave. Du coup j'enlève le 1er terme de la somme car il est nul, je transforme avec la formule que tu as mise, puis je simplifie en faisant disparaitre les k, il reste alors n et le coefficient binomial, je sors le n de la somme et dans la somme je transforme en utilisant le binome de new...

cassou44770 a écrit:Ne peut on pas simplifier k.(n/k) par n?

Si si j'avais pas compris dans ta phrase que tu avais fait apparaître du n/k

Pour ce qui est du rang je trouve que la matrice est de rang 2 pour m=-2 et m=1 Est ce juste ? Pour ce qui et du déterminant, si je développe ce que tu as trouvé cela me fait -m^3-m-2 Or, j'ai fait et refait mes calculs et je ne trouve pas l'erreur, je trouve encore -m^3 +3m-2 Je ne vois pas où es ...

En faisant le changement d'indice j=k-1 cela marcherait non? La somme irait de -1 à n-1 et comme on pourrait sortir n devant la somme et utiliser le binôme de Newton pour simplifier la somme Tu peux faire ce changement d'indice oui mais une somme indicée à -1 c'est peut-être pas très simple à manip...

Calculer 7^2008 modulo 15. J'ai trouvé 1 en utilisant la fonction indicatrice d'Euler, quelqu'un peut confirmer? Je trouve 1 également. Montrer que 7 divise 2222^5555+5555^2222. Je ne vois pas trop comment faire ça... Pour ce qui est de 2222^5555 : Commence par trouver un nombre x tel que 2222\equi...

@Zazz
non, tu sommes n fois le nombre 1, qu'obtiens-tu ?