25 résultats trouvés
Revenir à la recherche avancée
Luc a écrit:On obtient le module au carré.
Ce que tu dis est vrai si et seulement si le nombre complexe en question est de module 1.
bon je vais essayé de me débrouiller merci pour vos reponses
- par MrPatate
- 15 Sep 2012, 21:52
-
- Forum: ✯✎ Supérieur
- Sujet: module complexe
- Réponses: 4
- Vues: 538
SaintAmand a écrit:Alors augmente ta ration de poisson.
je me disais aussi que cétait trop simple du coup c'est pas:
lorsqu'on multiplie un complexe par son conjugué la partie imaginaire disparaît?
- par MrPatate
- 15 Sep 2012, 21:36
-
- Forum: ✯✎ Supérieur
- Sujet: module complexe
- Réponses: 4
- Vues: 538
Bonsoir j'ai un souci sur un exercice ou il faut déterminer le module et l'argument d'un complexe. z= (1-sin(a) + icos(a))/(1+ cos(a) - isin(a)) j'ai fait ceci: z= ( 1+ i(cos(a)+isin(a) )) / (1+ cos(a) -isin(a) ) z=(1+ iexp(ia))/(1+exp(-ia) z=( 1 + exp( i(pi/2 + a)) )/ (1+ exp(-ia)) j'ai ensuite mul...
- par MrPatate
- 15 Sep 2012, 20:52
-
- Forum: ✯✎ Supérieur
- Sujet: module complexe
- Réponses: 4
- Vues: 538
Mathusalem a écrit:Si la densité de courant J est constante, donc effectivement si le courant I est uniformément réparti.
oki

merci beaucoup pour le coup de main bonne soirée

- par MrPatate
- 20 Juin 2012, 21:06
-
- Forum: ⚛ Physique
- Sujet: Theoreme d'ampere.
- Réponses: 7
- Vues: 961
Mathusalem a écrit: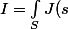 ds)
Qui réduit à I = JS seulement si J (la densité de courant) est ... ?
uniformément reparti?
- par MrPatate
- 20 Juin 2012, 18:48
-
- Forum: ⚛ Physique
- Sujet: Theoreme d'ampere.
- Réponses: 7
- Vues: 961
Pour le 1) si j'ai la même image que toi en tête, oui. Sinon tu poses ton pouce droit dans la direction du courant, et tes autres doigts te donne la direction de B. Pour le 2), au lieu d'utiliser le courant I, ils utilisent J = \frac{I}{\pi R^2} qui est la densité de courant. Quand tu prends un ann...
- par MrPatate
- 20 Juin 2012, 18:10
-
- Forum: ⚛ Physique
- Sujet: Theoreme d'ampere.
- Réponses: 7
- Vues: 961
Il suffit de poser I=J *(integrale)ds n'est ce pas?
j'ai trouvé ca par déduction... donc si quelqu'un pouvait valider^^
- par MrPatate
- 20 Juin 2012, 18:07
-
- Forum: ⚛ Physique
- Sujet: Theoreme d'ampere.
- Réponses: 7
- Vues: 961
bonsoir, j'ai un souci avec l'exercice suivant: On considere un conducteur cylindrique de rayon R et de longueur infinie traversé par un courant I. On suppose que la densité de courant par unité de surface est constante. 1) preciser en justifiant la reponse la direction et le sens du champ d'inducti...
- par MrPatate
- 20 Juin 2012, 17:54
-
- Forum: ⚛ Physique
- Sujet: Theoreme d'ampere.
- Réponses: 7
- Vues: 961
Bonjour, je suis en pleine révision du bac d'Histoire géo et j'ai pris un sujet dans mon livre pour m'entrainer: La France, centre des réseaux européens? Seulement je bloque vraiment. Est ce que qql peut me dire si j'ai bon? Voici mon plan: I- Avantages du teritoire français A) La France, Carrefour...
- par MrPatate
- 17 Juin 2012, 21:05
-
- Annonce globale: Composition en geographie
- Réponses: 1
- Vues: 1589
Bonsoir! Je suis étudiant, actuellement en deuxième années de licence mécaniques/physique des matériaux. A l'heure actuelle mes lacunes en math me pourrissent la vie dans quasiment toutes les matières... et ayant des objectifs plutôt haut il faut absolument que j'arrive à m'en sortir en math! Donc j...
- par MrPatate
- 11 Juin 2012, 21:43
-
- Forum: ✌ Présentez-vous
- Sujet: hello
- Réponses: 3
- Vues: 1119
Peacekeeper a écrit:Oui, y a un moment on atteint le régime de saturation, je pense. :dodo:
merci à tous pour votre aide en tout cas! et bonne soirée
- par MrPatate
- 11 Juin 2012, 21:31
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
Peacekeeper a écrit:sin(0)=0 :lol3:
oula c'est moche comme erreur en plus :mur: je crois que c'est le signal que j'ai bouffer trop de math ces derniers jours
- par MrPatate
- 11 Juin 2012, 21:26
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
Peacekeeper a écrit:J'ai fait le calcul de [(1/2)u + sin2u/4] de 0 a pi/2 et je trouve bien Pi/4...
N'oublie pas que c'est sin2u donc en Pi/2 on trouve sin(Pi)=0
oui je suis d'accord mais en 0 sin(2*0)=1 d'ou mon 1/4 en plus...
- par MrPatate
- 11 Juin 2012, 21:05
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
j'ai aussi un probleme sur la dernière étape. on pose cos²u= (1+cos2u)/2 (formule trigo) qu'on integre (1/2+(cos2u)/2 )du ===> [(1/2)u + sin2u/4] de 0 a pi/2 et l'application num donne: 1/2*pi/2 + sin(pi)/4 - (1/2*0 + sin 0 /4) = pi/4 - 1/4 soit au final ab*(pi/4 -1/4)*4 (pour avoir l'aire totale) e...
- par MrPatate
- 11 Juin 2012, 20:50
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
Peacekeeper a écrit:Ils effectuent un changement de variable en posant t=x/a. Je suis en train de chercher d'où vient le a devant l'intégrale...
si t²=a²/x² alors x=at donc dx=adt non?
d'ou le a
- par MrPatate
- 11 Juin 2012, 20:38
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
http://upload.wikimedia.org/wikipedia/fr/math/b/6/8/b684391b58c24cf38d3e13640e3adc5c.png j'ai un souci avec la deuxième étape pour moi on ne peux pas sortir le "a" de la racine ... et le passage de x a t reste obscure aussi... Et j'ai aussi un probleme sur la dernière étape. on pose cos²u...
- par MrPatate
- 11 Juin 2012, 20:14
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
Je ne me souviens plus exactement comment on fait, mais va faire un tour là-dessus c'est bien expliqué et c'est concis. :lol3: http://fr.wikipedia.org/wiki/Ellipse_%28math%C3%A9matiques%29 ok merci je vais voir ca. par contre du coup il y a une deuxième question dans l'exo (sinon c'es trop facile ^...
- par MrPatate
- 11 Juin 2012, 19:58
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
merci pur vos reponses.
Julie ta méthode me donne des boutons... mais je la garde pour plus tard!
je pensais plus a un méthode dans le style de ce que propose Peacekeeper, par contre j'ai toujours le même souci je vois pas comment poser le problème :mur:
- par MrPatate
- 11 Juin 2012, 19:51
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
chan79 a écrit:il y a une formule
aire =

ab
il s'agit de la démontrer ?
dans la question il dit calculer donc je pense que c'est ce que nous devons démontrer :/ ca métonnerait que sortir la formule suffise. Je pense qu'il faut passer pas une intégrale mais je vois pas du tout comment la poser...
- par MrPatate
- 11 Juin 2012, 18:57
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
Bonsoir je dois calculer l'aire de d'une ellipse dans le plan xy décrite par léquation: x²/a² +y²/b²=1 Et pour le coup je vois pas mais alors vraiment pas comment démarrer... et c'est pas le première foi que je but sur se genre de problème, auriez vous une méthode pour résoudre ce type d'exo? u au ...
- par MrPatate
- 11 Juin 2012, 18:12
-
- Forum: ✯✎ Supérieur
- Sujet: l'aire d'une ellipse
- Réponses: 28
- Vues: 7504
ab