Forum de Mathématiques: Maths-Forum

ptitnoir a écrit:si

alors (........)

Merci à vous deux pour votre aide, j'ai finalement abouti et compris, encore merci :lol3:

Bonjour, pour ma part, je ne me serai pas embrouillée avec les z barre. Tu sais que M appartient à C, donc les coordonnées de M vérifient l'équation de C, soit M(x, x/x-1). Donc z=x+i(x/x-1) Ensuite, tu calcules z² et tu remplaces tout ça dans Z=z²-2(1+i)z. En principe, si M' appartient à l'axe de ...

Calcule Z- \overline{Z} en remplacant dans cette expression petit z et petit \overline{z} par leur valeur en fonction de x (qui est un réel) ps) il faut connaitre les règles sur la contraposée d'une somme de 2 complexes et la contraposée d'un produit de 2 complexes et également que \overline{x+iy}=...

Attention à ne pas confonde petit z et GRAND Z z=x+i\frac{x}{x-1} , qui peut s'écrire aussi z =\frac{x}{x-1}(x-1+i) avec x un nombre réel donné différent de 1 Je t'aide en te montrant le calcul de la contraposée de petit z \overline{z}=(\frac{x}{x-1}) \overline{x-1+i}=( \frac{x}...

ptitnoir a écrit:C'est écrit dans mon message

Cet exercice consiste donc à montrer que

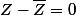
Donc sachant que z=x+i(x/(x-1)) je calcule Z puis Zbarre, ensuite Z-Zbarre et je dois trouver 0 ?

@Noisetteham Piste de Travail Utilise la propriété : le nombre complexe Z est un réel si et seulement si Z=\overline{Z} Cet exercice consiste donc à montrer que Z - \overline{Z}=0 Pour facilité les calculs , on a z=x+i\frac{x}{x-1} , et je te conseille d'utiliser z =\frac{x}{x-1}(x-1+i) De ...

Je ne vois pas du tout..

maths0 a écrit:Fais un dessin !

J'en ai déjà fait un, il ne m'aide pas plus que ça..

Pouvez-vous m'aider? :(

up pouvez vous m'aider :/

Pouvez vous m'aider svp, j'aimerais terminer cet exercice avant demain matin c'est important :/

Bonjour, merci pour votre réponse.

Oui mais je ne sais pas comment démontrer ''l'affixe z de M satisfait f'' c'est à dire la première partie de la démonstration..

Bonjour, je rencontre des difficultés sur cet exercice: Le plan est rapporté à un repère orthonormé direct (O;u;v) Soit (C) la courbe représentative de la fonction f définie sur R-{1} par f(x)=x/x-1 Au point M d'affixe z, on associe le point M' d'affixe Z=z²-2(1+i)z Démontrer que si M est un point d...

J'ai donc conclus que U est une suite géométrique de raison q=1.005 et de premier terme U0=V0+6000 or on sait que V0=1000 donc U0=7000 Donc pour tout n de N, Un=U0*q^n Un=7000*1.005^n Or pour tout n de N, Un=Vn+6000 donc Vn=Un-6000 Donc pour tout n de N, Vn=7000*1.005^n-6000 Est-ce correct?

Bonjour et merci pour votre réponse. Moi j'en suis à Un=Vn+6000 Un+1=Vn+1+6000 Un+1=1.005*Vn+30+6000 Un+1=1.005*Vn+6030 Mais je n'arrive pas à aboutir sur Un+1=q*un :hein: j'ai finalement Un+1=1.005(Vn+6000) donc Un+1=1.005*Un Est-ce correct?

Pouvez vous m'aider svp merci :triste:

Bonjour à tous, Alors voilà, j'ai un petit problème avec une question dans un exercice, cependant je vais le remettre en entier au cas où il y aurait d’éventuelles liaisons avec les deux premières questions ou d'éventuelles erreurs. 1) Soit la suite V définie sur N par V0=1000 et Vn+1=1.005*Vn+30. a...