Forum de Mathématiques: Maths-Forum

Bonsoir,

c'est où n est le nombre de pliage.

On te demande de trouver un ensemble de points qui vérifie une certaine propriété, du genre une droite, un cercle, un plan, un disque etc.
Oui,pour les deux premiers ensemble que tu cherches, tu n'as pas besoin de travailler sur f, tu travailles avec un complexe quelconque.

Et exp(i*Pi*x) non plus. Oui exactement, en n'oubliant pas la nature de et .

Bonjour,

pourquoi chercher une limite en 0 ? Cela n'a rien à voir ! D'où t'es venue cette idée ?
Ce qu'il faut faire, c'est regarder si f peut-être nulle, c'est à dire regarder si on peut trouver un complexe z tel que f(z)=0. Regarde bien ta fonction dans les yeux, c'est immédiat :)

Non, V est le volume de la lanterne, donc : V=volume cube+volume pyramide. Il n'y a plus qu'à appliquer les formules. Pour la question d'après, il faut calculer les valeurs de V(x) pour différentes valeurs de x, en partant de 0 et en allant jusqu'à 30, et en allant de 5 en 5: V(0)=..., V(5)=..., etc.

Ok ! Ben bon courage pour la suite :)

Oui c'est ça ! Au passage, tu n'avais pas besoin de résoudre 2 x + 1 = 0, tu l'as déjà fait à la question précédente ;)

Juste comme ça, t'es en quelle classe ?

Non. On te demande de résoudre, c'est à dire trouver toutes les valeurs de x telles que (2x-3)(4x²+4x+1)=0. Tu as écris P(x)=0.5 : c'est faux, P(x) dépend de x et vaut P(x)=(2x-3)(4x²+4x+1) ! Là, il faut résoudre une équation produit : pour (2x-3)(4x²+4x+1)=0, il faut quoi ? D'une part, que ....=0 o...

N'oublie pas les questions sont liées, et quand on te demande de factoriser, c'est pas que pour faire joli !

As-tu vraiment réfléchi à la D ? Regarde bien. Que vaut P(x) ? Qu'as tu déjà trouvé ?

Exact. Mais tu as 4x²+4x+1=(2x+1)². Pourquoi calculer un déterminant ??? Résoudre 4x²+4x+1=0, c'est la même chose que résoudre (2x+1)²=0 ! Et ne peux-tu pas résoudre (2x+1)²=0 sans calculer de discriminant ? C'était d'ailleurs le but de la question B, factoriser pour ensuite résoudre plus facilement...

Tu as fait une erreur de calcul. Mais réfléchis bien : tu as factorisé ton expression, tu as donc une autre forme qui permet de donner immédiatement les racines, pas besoin de sortir l'artillerie lourde ! Tu l'as trouvé toi même, on a 4x²+4x+1=(2x+1)² , n'en déduis-tu pas tout de suite les racines ?

Tu as une petite erreur dans ta factorisation, revérifie. Pour le C, tu dois bien sûr te servir de ta factorisation, te ramenant ainsi à une équation produit de degré 1.

C'est juste pour la hauteur h mais attention, n'appelle pas cette fonction f, mais h, comme le suggère l'énoncé. De même, le volume on te demande de l'appeler V.
Par contre tu as faux pour le volume, vois-tu pourquoi ? Comment as-tu fait pour trouver ça ?

Bonjour,

prenons l'exercice 2. La première question, as-tu su y répondre ? As-tu appris à te servir de ta calculatrice ?

oui tout à fait, moi pareil je m'étais créer des difficultés pour rien. A+

Si tu veux mathelot je vais essayé de lui expliquer je pense avoir compris maintenant ^^ \frac{\partial ^2 f}{\partial x^2}=\frac{\partial }{\partial x } \frac{\partial f}{\partial x} à partir de ça, tu dérives \frac{\partial f}{\partial x} en utilisant à la fois la formule classique de dérivée d'un...

Oui oui bien-sûr j'avais bien vu d'où ça venait (c'eût été assez horrible pour un maths sup de pas le voir) mais je voulais dire qu'avant que tu me donnes l'égalité je ne l'avais pas remarquée. Et puis j'avais jamais vu un cosinus défini sur C

Euh non mais pour cet exo ça m'a pas l'air vraiment utile si ?
Et puis on définit un cosinus complexe ? J'avais jamais vu ça ^^

J'ai un peu de mal à comprendre tout mais en tout cas merci ! Tu pense qu'en spé on verra tout ça ? Parce que je trouve qu'en sup on le développe pas trop... Donc finalement, quand tu calcules \frac{\partial ^2 F}{\partial u^2} on met cos v en facteur puisqu'il est constant, on applique la formule d...

Je fais mon erreur en calculant

En fait j'ai jamais calculé de dérivées parteilles secondes, d'où viennent les termes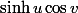 de ?