Forum de Mathématiques: Maths-Forum

maths0 a écrit:Exactement !
n=50 (entier naturel).

Ouii merci beaucoup pour ton aide!!! J'ai compris mon erreur du début!! Merci!

maths0 a écrit:Le modèle:

Ton exemple:

Je trouve cette équation: 5n²+9n-12950=0
delta=259081 et n=-51.8 ou n=50

maths0 a écrit:C'est fois, regarde la formule.
Tu as déjà la raison et le premier terme alors Un = ?
Au final ?

(n-3)+1(17+2+5n)/2=6456

maths0 a écrit:Avec Un= ? et U3 = ?

U3=17 et Un=Uo+nr

maths0 a écrit:Oui donc en appliquant la formule ? =6456

(n-3)+1(U3+Un)/2=6456???

maths0 a écrit:Non de l à m il y a: m-l+1 termes (dessus-bas)+1
De 3 à n il y a: ? termes

De 3 à n: (n-3)+1

Si on somme les termes de la suite \left( {{u_n}} \right) : De 0 à 0: \sum\limits_0^0 {{u_n}} = {U_0} : 1 terme De 0 à 1: \sum\limits_0^1 {{u_n}} = {U_0} + {U_1} : 2 termes De 0 à 2: \sum\limits_0^2 {{u_n}} = {U_0} + {U_1} + {U_2} : 3 termes De 0 à 3: \sum\limits_0^3 {{u_n}} = {U_0} + {U_1}...

maths0 a écrit:Combien il y a de terme en 3 et n ?

Je comprend pas désolé...

maths0 a écrit:Tu es d'accord on cherche n tel que: ?

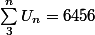
oui je suis ok

Pour une suite arithmétique, pour faire la somme du premier au dernier termes on utilise la formule suivante: 4$ \sum\limits_{premier}^{dernier} { = Nombr{e_{termes}} \times Moyenne = Nombr{e_{termes}} \times \frac{{premier + dernier}}{2}} Quel est le premier terme ici ? quel est le dernier ? combi...

chan79 a écrit:tu as



...

Si tu ajoutes tout membre à membre

6456=2(n-2)+5( ...
Tu continues avec une équation du second degré au passage
Ca s'arrange bien

Je comprend pas l'équation qu'on obtient au final

maths0 a écrit:C'est une équation à résoudre alors.

On m'a conseillé d'utiliser cette formule...

Pouvez-vous me dire si j'ai juste à cet exercice, mon résultat me parait bizarre...
Uest la suite arithmétique de raison 5 telle sue U0=2.
Il faut calculer n tel que U3+U4+...+Un=6456.
J'ai utilisé la formule: (n+1)(U0+Un)/2 ais je trouve 51873...

maths0 a écrit:28.4+28.4=56.8

Oui j'ai remarqué cette erreur mais le problème ne vient pas de là...

maths0 a écrit:Tu as mal résolu l'équation.

Je comprend pas mon erreur... Je recommence et je trouve 1.17
J'ai fais: (28.4-10r)+(28-5r)=38.8
28.4-10r+28.4-5r=38.8
56.4-15r=38.8
56.4-38.8=15r
17.6=15r
r=88/75=1.4

Jota Be a écrit:Oui c'est bien
Et si tu résous ceci, tu trouves la même chose que moi. Et même que je suis passé par une autre méthode, mais bon.

En utilisant cette méthode je ne trouve pas comme toi... quelle est ta méthode?

Jota Be a écrit:Bonjour,
C'est normal que r soit positive dans ce cas-là, je ne vois pas pourquoi tu te poses des questions.
Je trouve 6/5 comme raison, si je ne me suis pas trompé.

Comment tu as fais? Je ne trouve pas la même chose. J'ai fais: (U20-10r)+(U20-5r)=38.8 et j'ai résolu l'équation...

Bonjour, j'ai un exercice de maths à faire mais je ne suis pas sur de ce que j'ai fais. Voici l'énoncé: U est une suite arithmétique telle que U10+U15=38.8 et U20=28.4 Je dois trouver la raison. J'ai trouver r=94/75 mais ça me parait bizarre que que la raison soit positive alors que U20>U10+U15... Q...