Forum de Mathématiques: Maths-Forum

Merci pour vous tous les amis

S'il vous plait aidez moi à résoudre cet intégrale: ;)dx/(3+(2^x))

Bonjour,
Justifier la convergence de l'intégrale ;) ln(t).e^(-t) dt (l'intégrale entre 0 et +;))
Merci

S'il vous plait, j'ai besoin d'aide en cette question:
Quel est le nombre de diviseurs du nombre 15!
Et merci

[quote="Nightmare"]Bonsoir,

on peut utiliser simplement les définitions de nilpotente et d'inversible :

Si M est inversible et s'il existe k tel que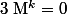 alors 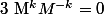, c'est à dire ce qui est absurde.
Oui ça se voit logique. Merci

Manny06 a écrit:utilise le determinant

Oui je vois; Merci bcp

Svp j'ai besoin d'une réponse:
Montrer que si A est nilpotente alors A n'est pas inversible.
Merci

Svp est ce que quelqu'un peut me donner la solution de cet exercice ?
Merci

Blueberry a écrit:il faut--> condition nécessaire. C'est bien ce que j'ai dit non ?

tu dis ( le terme général d'une série tend vers 0 => la série converge) ???

Je dirai même plus, il faut que ce qu'il y a sous le ln tende vers 1 car une série ne peut converger que si son terme général tend vers 0. Je ne suis pas d'accord avec toi à propos de ( une série ne peut converger que si son terme général tend vers 0) ; la série de terme général U_n = ln[1+(1/n)] d...

Physimath a écrit:A mon avis tu devrais utiliser les propriétés du ln pour avancer.

Oui je les ai utilisé mais je me suis bloqué U_n = ln[ n(n+2)^a (n+3)^b ] et après ???

Bonjour,

La série de terme général :
(n>=1) U_n = ln (n) + a ln (n+2) + b ln (n+3)
Trouver les valeurs de a et b pour lesquelles la série de terme général U_n converge et, dans ce cas, calculer sa somme.

Et merci

Autre méthode qui doit marcher :Merci sur trois entiers consécutifs, l'un d'eux (au moins) a un sinus plus grand que \frac{\sqrt2}2 en valeur absolue. \frac{|\sin(3k+1)|}{3k+1}+\frac{|\sin(3k+2)|}{3k+2}+ \frac{|\sin(3k+3)|}{3k+3}\geq\frac{\sqrt2}2\frac{1}{3k+3} \sum_{p=1}^{3...

Bonjour, Bonjour, On peut minorer le terme général par sin²(n)/n=1/(2n)-cos(2n)/(2n) Or le série de terme général cos(2n)/(2n) converge d'après le critère d'Abel, tandis que la série de terme général 1/(2n) diverge. Donc la série de terme général sin²(n)/n diverge et celle de terme général abs(sin(...

C'est clair maintenant.
Merci infiniment

Maxmau a écrit:Utilise la règle d'Abel pour montrer que la série de terme général cos2n/2n converge

Oui c'est ça, mais comment montrer la somme des cos(2n) est bornée ?

Maxmau a écrit:Bj
|sin(n)| > sin²n = (1 - cos2n)/2
Essaie de montrer que la série de terme général (sin²n/n) - (1/2n) est convergente

Moi aussi j'ai trouvé la même chose, mais le problème c'est de montrer (cos 2n)/2n est convergente ; et on a déjà 1/2n est divergente

Bonjour,
Svp j'ai besoin d'aide pour déterminer la nature de la série de terme général U_n = |sin n| / n
Merci

On résout {(\frac 1 2 )}^{\sqrt n} \le \frac 1 {n^2^} et on trouve que cela équivaut à \frac {\sqrt n} {log n} \ge \frac 2 {log 2} Vue la limite de \frac {\sqrt n} {log n} (qui est + \infty ), cette inégalité sera vraie à partir d'un certain rang n0 Donc à partir d'un certain rang, le terme...

Blueberry a écrit: n'est pas équivalent à 1/n² mais est majoré très vite par 1/n² à partir d'un certain rang (passer au log)

Svp est ce que vous pouvez mieux expliquer ?