12 résultats trouvés
Revenir à la recherche avancée
- 10 Avr 2012, 01:44
- Forum: ✎✎ Lycée
- Sujet: Besoin d'aide avec les logarithmes...
- Réponses: 8
- Vues: 781
Besoin d'aide avec les logarithmes...
Bonjour,
Je dois déterminer la valeur de x dans:

Voici ce que j'ai réussi à faire:

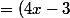log5 = (x+2)log125)


Quelqu'un pourrais m'aider? Je suis complètement bloqué...
Merci!
Je dois déterminer la valeur de x dans:
Voici ce que j'ai réussi à faire:
Quelqu'un pourrais m'aider? Je suis complètement bloqué...
Merci!
- 09 Avr 2012, 16:20
- Forum: ✎✎ Lycée
- Sujet: Besoin d'aide avec les logarithmes...
- Réponses: 8
- Vues: 781
Après autant d'erreurs, je comprends que tu puisses avoir un doute. Or tu ne devrais avoir aucun doute concernant ton résultat. Un calcul n'est pas une suite de devinettes, il obéit à des règles (de calcul). Si tu les appliques ton calcul est juste. Sinon il est faux. À part ça c'est juste si tu ra...
- 23 Mar 2012, 20:32
- Forum: ✯✎ Supérieur
- Sujet: factorisation et simplification
- Réponses: 9
- Vues: 710
C'est mieux. Il reste le problème à la dernière ligne. Un problème de simplification de fractions si tu veux mon avis... \frac{6x^3-15x^2+2xy-5y}{12x^2y+4y^2} \frac{(6x^3+2xy)-(15x^2+5y)}{4y(3x^2+y)} \frac{2x(3x^2+y)-5(3x^2+y)}{4y(3x^2+y)} \frac{2x-5}...
- 23 Mar 2012, 15:56
- Forum: ✯✎ Supérieur
- Sujet: factorisation et simplification
- Réponses: 9
- Vues: 710
Dans le cas où - je précise bien - tu chercherais à écrire des égalités entre les différentes expressions, il y a une erreur à la troisième ligne et une autre à la quatrième. Ok, donc: \frac{6x^3-15x^2+2xy-5y}{12x^2y+4y^2} \frac{(6x^3+2xy)-(15x^2+5y)}{4y(3x^2+y)} \frac{2x...
- 23 Mar 2012, 00:52
- Forum: ✯✎ Supérieur
- Sujet: factorisation et simplification
- Réponses: 9
- Vues: 710
ev85 a écrit:Valider quoi ?
Si c'est pour savoir si ces quatre expressions sont égales c'est non. Tu as donc bien fait de résister à la tentation d'écrire des signes = entre elles.
e.v.
Dans se cas, où se trouve mon erreur? Je dois simplifier la première expression...
Merci!
- 22 Mar 2012, 21:36
- Forum: ✯✎ Supérieur
- Sujet: factorisation et simplification
- Réponses: 9
- Vues: 710
factorisation et simplification
Bonjour,
Est-ce que quelqu'un pourrait valider svp?

-(15x^2+5y)}{4y(3x^2+y)})
-5(3x^2+y)}{4y(3x^2+y)})
-5}{4y})
MERCI!!!
Est-ce que quelqu'un pourrait valider svp?
MERCI!!!
- 22 Mar 2012, 20:40
- Forum: ✯✎ Supérieur
- Sujet: factorisation et simplification
- Réponses: 9
- Vues: 710
Non non =) si tu places le signe moins au numérateur, cela te fait juste passer de \frac{-3\sqrt{2} -6 + (\sqrt{2}+2)x}{-2} à \frac{3\sqrt{2} +6 - (\sqrt{2}+2)x}{2} Merci!!! Je suis de retour aux études et mes mathématiques sont très loin dans ma mémoire qui semble faire défaut!
- 14 Mar 2012, 01:26
- Forum: ✯✎ Supérieur
- Sujet: rationalisez le dénominateurs
- Réponses: 5
- Vues: 566
Salut =) C'est une petite faute faite en recopiant, à l'avant dernière ligne du développement, qui t'a induit en erreur ^^ Ensuite, tu n'as qu'à faire passer le signe négatif au numérateur pour obtenir l'expression voulue ! Julie :) Donc \frac{-3 + x}{\sqrt{2}-2} \frac{(-3 + x)(\sqrt{2}...
- 13 Mar 2012, 21:09
- Forum: ✯✎ Supérieur
- Sujet: rationalisez le dénominateurs
- Réponses: 5
- Vues: 566
rationalisez le dénominateurs
Salut, Comment puis-je rationalisez le dénominateurs de l'expression suivante: \frac{-3 + x}{\sqrt{2}-2} Voici ce que j'ai fait mais je suis bloqué: \frac{-3 + x}{\sqrt{2}-2} \frac{(-3 + x)(\sqrt{2}+2)}{(\sqrt{2}-2)(\sqrt{2}+2)} \frac{-3\sqrt{2} - 6 + x\sqrt{2} + 2x}{...
- 13 Mar 2012, 20:31
- Forum: ✯✎ Supérieur
- Sujet: rationalisez le dénominateurs
- Réponses: 5
- Vues: 566
J'ai trouvé le même résultat que toi : l'erreur est dans l'énoncé (à moins d'un oubli connexe). Avec du LaTeX , on améliore aussi la lisibilité : [\frac{2}{5} *(\frac{3}{8} + \frac{4}{5} * (-\frac{2}{3}))] *{ \frac{3}{2}} = [\frac{6}{10} *(\frac{45 - 64}{120} * \frac{3}{2})]...
- 13 Mar 2012, 16:40
- Forum: ✯✎ Supérieur
- Sujet: Besoin d'aide sur la résolution d'une équation
- Réponses: 3
- Vues: 559
Besoin d'aide sur la résolution d'une équation
Bonjour, Je suis de retour aux études depuis peu et je bûche sur un problème mathématique... Je dois évaluer l'expression suivante: [ 2/5 ( 3/8 + 4/5 X ( -2/3 ) ) ] ÷ 2 1/3 La réponse devrait être -19/700 mais je n'arrive pas à cette réponse :mur: . Quelqu'un peut m'indiquer où se trouve mon erreur?...
- 13 Mar 2012, 16:10
- Forum: ✯✎ Supérieur
- Sujet: Besoin d'aide sur la résolution d'une équation
- Réponses: 3
- Vues: 559
- 12 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
