145 résultats trouvés
Revenir à la recherche avancée
Famille libre
Bonjour, Voici ce qui me pose problème : Soit la famille (M1, M2, M3) où M1 = (-1 2 -1 et M2 = (2 -2 1 et M3 = ( 0 0 2 -1 2 -1 1 -1 1 0 0 1 0 0 0) 0 0 1) 0 0 0) On souhaite montrer que cette famille est libre. La correction donne soient (L1, L2, L3) E R3 tels que L1M1 + L2M2 + L3M3 = 0. implique le ...
- 28 Aoû 2015, 16:48
- Forum: ✯✎ Supérieur
- Sujet: Famille libre
- Réponses: 1
- Vues: 281
deltab a écrit:Bonjour
Pourquoi n'as tu pas fait ce que je t'ai demandé?
Même avec l'erreur sur, on a
Mais c'est la même chose que ça Un = ((e^(-1/2))^n)*2(-1+e^(1/2)) (j'avais mal mit les parenthèses) mais je ne comprenais pas comment trouver à quoi correspondais q.
- 15 Aoû 2014, 17:24
- Forum: ✯✎ Supérieur
- Sujet: Suite
- Réponses: 12
- Vues: 687
Sake a écrit:Oui mais c'est pas ça qui est intéressant...
On voit surtout que u_{n+1} = e^{-1/2}*u_n, et c'est juste assez
Ah oui, merci. Je n'arrive pas à voir ce genre de chose.
- 15 Aoû 2014, 17:10
- Forum: ✯✎ Supérieur
- Sujet: Suite
- Réponses: 12
- Vues: 687
Bonjour. As-tu montré que [U_n-\alpha| \le \left(\frac{2}{3}\right)^n[U_0-\alpha| ? Si OUI , ce n'est pour rien que j'ai appelé la valeur de U_0 et la valeur approchée de \alpha . Si NON , commences par le montrer (par récurrence)!! Oui, je l'ai montré. Donc [U_n-\alpha| \le \left(\frac...
- 15 Aoû 2014, 17:02
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une suite
- Réponses: 29
- Vues: 1068
- 15 Aoû 2014, 16:41
- Forum: ✯✎ Supérieur
- Sujet: Suite
- Réponses: 12
- Vues: 687
- 15 Aoû 2014, 16:36
- Forum: ✯✎ Supérieur
- Sujet: Suite
- Réponses: 12
- Vues: 687
- 15 Aoû 2014, 16:18
- Forum: ✯✎ Supérieur
- Sujet: Suite
- Réponses: 12
- Vues: 687
Erreur de frappe de la part de ton corrigé. C'est pourtant simple : tg(x) = sin(x)/cos(x) donc 1 + tg(x) = 1 + sin(x)/cos(x) = [cos(x) + sin(x)]/cos(x) et en prenant le ln... Edit : Il n'y a jamais de formule toute prête en maths, sauf dans des cas triviaux où il faut connaître des "formules p...
- 15 Aoû 2014, 15:48
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 8
- Vues: 728
Remarque que ln(1 + tg(x)) = ln(cos(x) + sin(x)) - ln(cos(x)), puis utilise la linéarité de l'intégration (sur un segment) pour l'addition. Mais je n'ais jamais vu cette formule en fouillant sur internet ( http://perso.ens-lyon.fr/francois.le_maitre/data/documents/colles/colle-16_calculs-d-integral...
- 15 Aoû 2014, 14:27
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 8
- Vues: 728
Bonjour. En t'aidant de la question 5.c), montre par récurrence que pour tout n \in \mathbb{N}^* , [U_n-\alpha| \le \left(\frac{2}{3}\right)^n[U_0-\alpha| . (N'oublies pas U_0=1 et \alpha\sim 1.26 (donné dans l'énoncé.) Que peux-tu en déduire? Je ne vois pas ce que l'on peut en déduire, mai...
- 15 Aoû 2014, 13:36
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une suite
- Réponses: 29
- Vues: 1068
cuati a écrit:Je pense que tu ne sais pas encore tout à fait faire un changement de variable...
En posant, on a
et ce dernier signe moins compense l'inversion des bornes...
ok merci et je ne vois pas en quoi la 3) peut aider à répondre à la 4) ?
- 15 Aoû 2014, 12:55
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 8
- Vues: 728
deltab a écrit:Bonjour.
En t'aidant de la question 5.c), montre par récurrence que pour tout,
. (N'oublies pas
et
(donné dans l'énoncé.) Que peux-tu en déduire?
J'ai réussi merci
- 15 Aoû 2014, 12:53
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une suite
- Réponses: 29
- Vues: 1068
cuati a écrit:Pour la 8, il suffit de multiplier les inégalités de 6 par n et de se servir ensuite de la 7.
mais faut'il se servir de la 4) pour remplacer 1/2(In-1+In) car je ne trouve pas la même limite de chaque côté et je ne vois pas comment faire autrement
- 15 Aoû 2014, 10:23
- Forum: ✯✎ Supérieur
- Sujet: Primitive
- Réponses: 5
- Vues: 566
Bonjour Vraiment! \ln([1;e])=[0,1] et non [1;e] ok donc la réponse est simplement : g([1;alfa])=[g(1);g(alfa)]=[ln(3);alfa] car g est continue et monotone sur [-1/2;+infini] et donc sur [1;alfa] ; de plus Uo=1 donc Un C [1;alfa] car 1<ln(3) Je n'arrive pas à répondre à la question de la que...
- 15 Aoû 2014, 08:44
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une suite
- Réponses: 29
- Vues: 1068
Suite
Bonsoir,
https://mega.co.nz/#!mFYAFRQZ!JrqT3k4PVL8sObBBJAW5nEEUTEBycAMxLV235P0WUjE
Pour la 1), je trouves 2e^(-n/2)(-1+e^(1/2)) mais je n'arrive pas à répondre à la 2).
Merci de votre aide
https://mega.co.nz/#!mFYAFRQZ!JrqT3k4PVL8sObBBJAW5nEEUTEBycAMxLV235P0WUjE
Pour la 1), je trouves 2e^(-n/2)(-1+e^(1/2)) mais je n'arrive pas à répondre à la 2).
Merci de votre aide
- 14 Aoû 2014, 21:43
- Forum: ✯✎ Supérieur
- Sujet: Suite
- Réponses: 12
- Vues: 687
deltab a écrit:Bonsoir.
Quelle est l'image d'un intervallepar une fonction continue et monotone sur
?
[a;b] je penses
- 14 Aoû 2014, 21:39
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une suite
- Réponses: 29
- Vues: 1068
Bonjour, pour la 7) ce n'est pas cela. Indication : dans I_n+I_{n+1} factorise le numérateur par e^{-(n+1)x} ensuite des choses se simplifient et c'est assez simple. Pour la 8) il suffit d'utiliser la 6) et la 7). Bon courage. merci, du coup, je trouve (e^(-n-1))-1/(-n-1) pour la 8 je m'en ...
- 14 Aoû 2014, 17:06
- Forum: ✯✎ Supérieur
- Sujet: Primitive
- Réponses: 5
- Vues: 566
cuati a écrit:C'est faux lorsque u est elle même une fonction différente de...
2. Faire le changement de variabledans l'intégrale J.
avec le changement de variable je trouve J = I avec les bornes inversées ce qui reviens à mon résultat précédent
- 14 Aoû 2014, 16:53
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 8
- Vues: 728
Primitives
Bonjour,
https://mega.co.nz/#!LJwj0Yaa!E9g4vlUjW5P5KdxV_4HMWMyBHDq9zc3JnOyPZVYG7I4
pour la 2, j'ai utilisé (uln(u)-u)'=ln(u) et je trouve I = -J
merci de votre aide
https://mega.co.nz/#!LJwj0Yaa!E9g4vlUjW5P5KdxV_4HMWMyBHDq9zc3JnOyPZVYG7I4
pour la 2, j'ai utilisé (uln(u)-u)'=ln(u) et je trouve I = -J
merci de votre aide
- 14 Aoû 2014, 16:33
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 8
- Vues: 728
5) Question 5-b) Étudies le signe de la fonction =g(x)-x) sur
sur  . Que peut-on conclure sur le signe de
. Que peut-on conclure sur le signe de 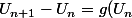-U_n) ?
?
U'(x)=g'(x)-1
pour tout x appartenant [1;alfa], 00
U'(x)=g'(x)-1
pour tout x appartenant [1;alfa], 00
- 14 Aoû 2014, 15:50
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une suite
- Réponses: 29
- Vues: 1068
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
