Forum de Mathématiques: Maths-Forum

PS : r est un entier strictement supérieur à 1 et la matrice est de taille n x n (n entier supérieur à 1)

\begin{pmatrix} 1 & 1 & \cdots & 1 &1 \\ r & 1 & \cdots & 1 & 1 \\ \vdots & \ddots & \ddots & & \vdots \\ r & r & \cdots & r & 1\end{pmatrix} Bonjour, je cherche à calculer les valeurs propres de cette matrice, mais je n'arrive pas à c...

On dispose sur la table 38 allumettes. Deux joueurs A et B prennent chacun leur tour un nombre d'allumettes compris entre 1 et 4. Le joueur qui prend la dernière allumette a perdu. Le joueur qui commence et qui joue avec une stratégie bien définie, peut gagner la partie à coup sûr. Trouver et justif...

Quel est le reste dans la division par 7 du nombre
999888777666555444333222111 ?
_________

Je pense bien à une décomposition avec 111 et 10^3, mais à part ça...
Merci à ceux qui pourront m'aider.

Ok, ça y est je viens de comprendre - merci, c'est sympa.
:zen:

Bonsoir à toi (et merci de m'aider :++: )

j'ai pu montrer que (mod.9), mais je ne sais pas trop quoi en faire :hein:

N est un entier naturel écrit en base 10, on appelle S la somme de ses chiffres.
Démontrer que N est congru à S modulo 9.

Voilà. Toute idée est la bienvenue !!! :we:

Je te le fais pour la première : la fonction est continue sur ]0;1] et admet une limite en 0 qui vaut 1 (à montrer) elle est donc prolongeable par continuité en une fonction continue sur [0;1]. Et il n'y a aucun problème à integrer une fonction continue sur un compact... Merci beaucoup, j'ai juste ...

Oui, on peut prolonger les integrande par continuité en 0 (c'est des taux d'accroissements) cela revient donc a integrer des fonctions continues sur des compacts... euh... d'accord, je comprends que tu me parles là du problème en 0, mais est-ce que je le justifie comme ça ? Et sinon, y a pas d'autr...

Bonsoir à tous, je sais que ça va paraître assez évident pour beaucoup d'entre vous, mais j'ai toujours du mal ( :hum: ) avec ce genre de questions : 1) Montrer que \int_{0}^{1} \frac{1-e^{-x}}{x}\, dx existe. 2) Montrer que \forall n \in IN*, l'intégrale I_n = \int_{0}^{1} \frac{1}{x} (1-(1...

Merci Tize, je viens seulement de reprendre ça ... et ça marche ! :++:

Ah oui, M c'est la matrice bien sûr !

\begin{bmatrix} a_1-x & \beta-x & \beta-x & \cdots & \beta-x \\ \alpha-x & a_2-x & \beta-x & \cdots & \beta-x \\ \alpha-x & \alpha-x & a_3-x & \cdots & \beta-x \\ \vdots & & \ddots & & \vdots \\ \alpha-x & \alpha-x & \alpha-x &...

Bon, je trouve (aux erreurs de calcul près) :



(avec tes notations)
euh... ça donne quoi comme matrice ? :dingue:

Flodelarab a écrit:(1,0,-1) ???

parfait
ton équation de plan est donc:
1x+0y-1z+d=0

x-z+d=0

reste plus qu'a fixer d

MERCI KI ?

EDIT: réponse x-z+1=0

J'arrive à la même chose.

Tu es sûr que tu ne t'es pas trompé en remplaçant ? Il faut remplacer x, y et z par les coord. et non a, b et c.

:id:
Je me lance ! Merci pour le déblocage !

La forme générale d'une équation de plan est ax + by + cz = d
Il faut écrire le système vérifié par cette éq. appliquée aux coordonnées de A, puis C, puis D.

En espérant que ça peut t'aider...

Soit E le IR-ev des polynômes de degé inférieur ou égal à 2. Soit \phi l'endomorphisme de E défini par pour tout p de E et pour tout x de IR par : \int_{0}^{1} [ap(t)+bxtp'(x-t)+cx^2t^2 p^{(2)}(x-t)]\, dt où a, b et c sont des réels. Soit la base canonique de E \b...

J'avais bien remarqué que exp(racine cubique de 3x) est la fonction réciproque de , c'est ok par ailleurs pour les bornes, mais est-ce que ça veut dire que 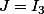? Tu pourrais me détailler pourquoi exactement ?

Merci de ton aide, c'est sympa de ta part. :happy2: