Forum de Mathématiques: Maths-Forum

maths0 a écrit:Regarde un exemple de ton cours.

Je n'y arrive vraiment pas :/

:hum:

maths0 a écrit:Si tu écris: g(x)=0 solution alpha unique sur R.
Tu commences par la conclusion ?

Je ne vois pas vraiment comment faire alors..

C'est un peu le bazard plus haut, quelle est ta réponse pour: IV- 1) Démontrer que l'équation g(x)=0 admet une solution unique alpha sur R. g(x)=0 solution alpha unique sur R g(x)=3e^(-x)+e(-x)+2=0 e^(x) (3+x+2e^x)=0 g(x) continue sur ]-infini;-2] et croissante sur ]-infini;-2] 0 Appartient a ]-inf...

maths0 a écrit:Et en -l'infini ?

+ infini
Effectivement je me suis trompé en recopiant à l'autre message.
Et désolé pour le "F5" ^^

maths0 a écrit:Il y a des problèmes sur tes limites quelles sont tes calcules ?
Logiquement si g est "décroissante sur ]-2;+ l'infini[" en général en +00 ça limite ne vaut pas +00.

Ma limite en +infini j'ai trouvé 2

Il y a vraiment personne? :hum: :hum:

Bonjour, J'ai eu un jour de plus. Alors j'ai fait toute la première partie: Voila ce que j'ai trouvé: I-Lim en + l'infini = + l'infini Lilm en - l'infini = 2 II- J'ai bien trouvé III- g(x) est croissante sur ]- l'infini;-2] et décroissante sur ]-2;+ l'infini[ IV- 1) g(x)=0 solution alpha unique sur ...

On a lim x;););) de e^(;)x) = lim X;)+;) de e^(X) = +;). Comme d’autre part
lim x;););) (3 + x) = +;), on a lim x;););) de (3+x)e^(;)x) = +;) Soit lim x;););) de g(x)= +;)
:help:

maths0 a écrit:Où est la forme indéterminée ?

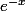
Quelle est la limite en + et - l'infinie de ? :hum:

4$g(x) = 3{e^{ - x}} + x{e^{ - x}} + 2 La limite d'une somme est la somme des limites ici ... Factorise débrouille toi pour mettre sous une forme connue. Exact seulement je n'arrive pas à trouver la limite en de: e^(-x) Je sais que ça tend vers 0 (j'ai vérifié avec MAPLE), mais je n'arrive ...

Bonsoir, Attention , ce forum n’a pas pour but de fournir des corrections de devoirs aux élèves. Les utilisateurs souhaitant vous aider s’efforceront de vous expliquer comment parvenir au résultat attendu sans toutefois vous y conduire directement. Par ailleurs, il est apprécié que les élèves expos...

Bonjour à tous,je suis en terminale S. Je viens faire appel à votre aide car je dois rendre un DM pour lundi et je suis très en retard à cause de grave souci de santé, et bloqué sur des questions. Je suis pas ici pour recevoir de la pitié. Je demande juste de l'aide, Et sachez que je fais vraiment m...