3930 résultats trouvés
Revenir à la recherche avancée
Re: Fonction limite et suite
soit f croissante sur un intervalle I :  < f(b))
- 10 Nov 2021, 14:29
- Forum: ✯✎ Supérieur
- Sujet: Fonction limite et suite
- Réponses: 16
- Vues: 522
Re: Fonction limite et suite
Sens de variation de u_n C'est un peu long , il y a peut-être une méthode plus directe ? u_{n+1}-u_n= 3-\frac{1}{u_n+1}-u_n Après réduction au même dénominateur (j'ai la flemme de taper les calculs intermédiaires) : u_{n+1}-u_n= \frac{-u_n^2+2u_n+2}{u_{n+1}} qui est du signe de -u_n^2+2u_n+2 Ce tri...
- 10 Nov 2021, 12:08
- Forum: ✯✎ Supérieur
- Sujet: Fonction limite et suite
- Réponses: 16
- Vues: 522
Re: Fonction limite et suite
Pourquoi entre Un + 1 >1 et 1/Un <1, le +1 n'y est plus
oui, erreur de frappe
dans les lignes 3 à 5 remplacer
- 10 Nov 2021, 10:57
- Forum: ✯✎ Supérieur
- Sujet: Fonction limite et suite
- Réponses: 16
- Vues: 522
Re: Fonction limite et suite
Bonjour,
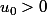
supposons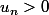 et montrons que
et montrons que  est positif
est positif
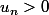
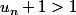
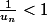
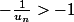
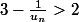
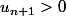
Par récurrence sur ,
,  est positif
est positif
supposons
Par récurrence sur
- 10 Nov 2021, 10:22
- Forum: ✯✎ Supérieur
- Sujet: Fonction limite et suite
- Réponses: 16
- Vues: 522
Re: Trouver la fonction exposant
@lazare
=f(x)f(0))
Tu ne vois vraiment pas ce que vaut) ?
?
Et tu ne sais pas factoriser ?
Tu ne vois vraiment pas ce que vaut
Et tu ne sais pas factoriser ?
- 05 Nov 2021, 08:48
- Forum: ✯✎ Supérieur
- Sujet: Trouver la fonction exposant
- Réponses: 13
- Vues: 762
Re: dissertation de philosophie sur le temps
Si quelqu'un pouvait m'aider
- 04 Nov 2021, 18:34
- Forum: ✎✎ Lycée
- Sujet: dissertation de philosophie sur le temps
- Réponses: 21
- Vues: 1114
Re: Limite de suite
Effectivement, après le signalement de ce multipost, on regrette d'avoir perdu son temps...
Est-ce que Jilbert est coutumier du fait ?
Est-ce que Jilbert est coutumier du fait ?
- 04 Nov 2021, 18:11
- Forum: ✎✎ Lycée
- Sujet: Limite de suite
- Réponses: 7
- Vues: 374
Re: Limite de suite
Variante utilisant le théorème des suites adjacentes : 2 suites adjacentes ont même limite (2 suites sont adjacentes si l'une croit et l'autre décroit et leur différence tend vers 0) v_1=10,5 u_1=11,6 on a donc v_0<v_1<u_1<u_0 Supposons l'inégalité : v_{n-1} <v_n<u_n<u_{n-1} Montrons qu'alors : v_n...
- 04 Nov 2021, 18:04
- Forum: ✎✎ Lycée
- Sujet: Limite de suite
- Réponses: 7
- Vues: 374
Re: Limite de suite
Bonjour,
Il faut montrer, par un raisonnement par récurrence, que :
- est décroissante
est décroissante
- est croissante
est croissante
-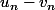 tend vers 0
tend vers 0
alors ces 2 suites sont adjacentes et ont la même limite.
Tu n'as pas d'autres indications ?
Il faut montrer, par un raisonnement par récurrence, que :
-
-
-
alors ces 2 suites sont adjacentes et ont la même limite.
Tu n'as pas d'autres indications ?
- 04 Nov 2021, 15:40
- Forum: ✎✎ Lycée
- Sujet: Limite de suite
- Réponses: 7
- Vues: 374
Re: Trouver la fonction exposant
Soit f(a+b) =f(a)f(b) Comment à partir de cette égalité peut on démontrer que est une fonction exposant? Re-bonjour, Tout d'abord ce n'est pas simplement une égalité mais une identité c'est à dire \forall(a,b) \in R^2, f(a+b)=f(a)f(b) Je me pe...
- 03 Nov 2021, 12:00
- Forum: ✯✎ Supérieur
- Sujet: Trouver la fonction exposant
- Réponses: 13
- Vues: 762
Re: Trouver la fonction exposant
Je reformule ta question. Trouver la (les) fonction(s) f vérifiant l'équation : quelqes soient (a,b) \in R^2 f(a) f(b) = f(a+b) En évaluant f en une valeur bien choisie de b tu peux montrer que f0) =1 Ce que tu appelles fonction exposant n’est autre que la fonction ex...
- 02 Nov 2021, 20:14
- Forum: ✯✎ Supérieur
- Sujet: Trouver la fonction exposant
- Réponses: 13
- Vues: 762
Re: Exercice racines n-ième d'un nombre complexe
En multipliant ’haut et bas’ z par le conjuguė de son dénominateur :
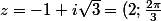)
- 31 Oct 2021, 19:00
- Forum: ✯✎ Supérieur
- Sujet: Exercice racines n-ième d'un nombre complexe
- Réponses: 7
- Vues: 416
Re: Math fine , financière, mathématiques
Bonjour
C'est quoi le hadj ?
C'est quoi le hadj ?
- 14 Oct 2021, 06:51
- Forum: ✎✎ Lycée
- Sujet: Math fine , financière, mathématiques
- Réponses: 5
- Vues: 634
Re: équation du second degré
On n'"enlève pas le carré" mais on applique 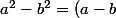(a+b))
- 27 Sep 2021, 22:13
- Forum: ✎✎ Lycée
- Sujet: équation du second degré
- Réponses: 4
- Vues: 424
Re: Montrer qu'un système AX=B admet une unique solution
Solution unique 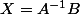 car système de Cramer puisque le déterminant de la matrice A n'est pas nul
car système de Cramer puisque le déterminant de la matrice A n'est pas nul
- 27 Sep 2021, 12:49
- Forum: ✯✎ Supérieur
- Sujet: Montrer qu'un système AX=B admet une unique solution
- Réponses: 1
- Vues: 575
Re: Suite arithmétique
Que peux-tu conclure du calcul de 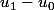 et
et 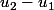 ?
?
- 08 Sep 2021, 16:42
- Forum: ✎✎ Lycée
- Sujet: Suite arithmétique
- Réponses: 4
- Vues: 401
Re: DM de PCSI sur les limites et développements limités de
Bonsoir
Tu es vraiment en PCSI ?
Tu es vraiment en PCSI ?
- 10 Mar 2021, 19:20
- Forum: ✯✎ Supérieur
- Sujet: DM de PCSI sur les limites et développements limités de fonc
- Réponses: 17
- Vues: 1059
Re: décomposition fraction rationnelle
Bonsoir
Commence par lire un cours sur la décomposition en éléments simples ...
Il y en a plein sur internet.
Commence par lire un cours sur la décomposition en éléments simples ...
Il y en a plein sur internet.
- 10 Mar 2021, 19:16
- Forum: ✯✎ Supérieur
- Sujet: décomposition fraction rationnelle
- Réponses: 11
- Vues: 481
Re: Un devoir maison
OK, là l'énoncé est maintenant correct
C'est curieux car Kermouche renvoie exactement le même énoncé (copier-coller) sans prendre la peine de le corriger et il est correct !
C'est toujours un bon exercice que de corriger ses fautes d'orthographe ...
- 09 Mar 2021, 17:01
- Forum: ✎✎ Lycée
- Sujet: Un devoir maison
- Réponses: 21
- Vues: 601
Re: Valeur moyenne d'une fonction continue
Bonjour, Au temps pour moi ! J'ai mal interprété l'énoncé, ma réponse concernait les fonctions f et f^2 qui ont même valeur moyenne sur tout intervalle de leur domaine de définition (commun). Sur [0;1], 0\leq\frac{4x}{9}\leq \frac{2x}{3} et pourtant leur valeur moyenne est la même. Ce n'est pas grap...
- 09 Mar 2021, 16:34
- Forum: ✎✎ Lycée
- Sujet: Valeur moyenne d'une fonction continue
- Réponses: 12
- Vues: 645
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
