Forum de Mathématiques: Maths-Forum

Pauloo a écrit:C'est ça ?

Oups erreur de calcul. Cela fait donc:

sin(Pi/4 + Pi/3) = (rac2)/2*1/2 + (rac3)/2*(rac2)/2 = (rac6 + rac2) / 4

Pauloo a écrit:Donc la bonne réponse est la réponse C)

C'est ça ?

Pauloo a écrit:Ce qui fait environ 0.032

Donc la bonne réponse est la réponse C)

Dinozzo13 a écrit:Du coup, ça change pas grand chose, tu as :
.

Ce qui fait environ 0.032

Dinozzo13 a écrit:Ah oui, je comprend mieux :hum:




Un coup tu mets pi/4, un coup tu mets pi/2.
Pas étonnant qu'on s'emmêle les pinceaux.

Ah oui mince, c'est bien sin(Pi/4 +Pi/3)

Pauloo a écrit:Donc je vois pas quelle est la bonne réponse..

Comment dois-je faire ?

Dinozzo13 a écrit:Ok, mais quelle est l'utilité ?
'y a pas de sin(pi/4) ...

Enfin, bref.

Donc je vois pas quelle est la bonne réponse..

[quote="Dinozzo13"]J'aimerais d'ailleurs savoir comment tu fais pour obtenir ces valeurs ?
Penses-tu que et ?[/Q

sin(Pi/4)= rac2/2 et sin(Pi/3)=rac3/2 selon les formules de mon cours

manoa a écrit:moi pas d'accord.
pourrais tu nous montrer comment tu arrive à ce résultat ?

Pour moi , sin(pi/2 + pi/3) = rac2 / 2 + rac3/2 = (rac2+rac3)/2
Mais j'ai des doutes...

Bonjour , voici mon problème

sin(Pi/4 + Pi/3)= A) (rac2-rac6)/4 B) (rac6+rac2)/4 C) (rac2+rac6)/2 D) (rac2+rac3)/2

J'ai repondu réponde D, (rac2+rac3)/2
Êtes vous d'accord ?
Merci d'avance

chan79 a écrit:Tiens, pour moi, ça semble coller

[img][IMG]http://img805.imageshack.us/img805/2485/azeh.png[/img][/IMG]

Oui, j'ai aussi reproduit le schéma, ça fait bien 1.4cm. Merci pour votre aide

Pauloo a écrit:Donc comme cosBOC=0.28 , cosBOC = cosCOD

Mais si cosBOC= 0.28
A'C'=AC*0.28
=5*0.28= 1.4 or sur la feuille cela ne semble pas logique

chan79 a écrit:non, c'est -(-0.28)=0.28

Donc comme cosBOC=0.28 , cosBOC = cosCOD

chan79 a écrit:il est supplémentaire avec COD (il suffit de changer le signe)

Donc cosBOC= -0.28?

chan79 a écrit:BD=5 et cos COD=-0.28
A'C'=AC*cos(BOC)= ...

Comment calcule-t-on cos BOC ?

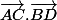
chan79 a écrit:si O est le milieu des diagonales, =AC.BD*cos COD
tu en déduis cos COD
puis A'C' se déduit de AC en multipliant par un cosinus

Je fais donc
AC.BD=AC.BD.cosCOD
-7=5*-5*cosCOD
-7/-25= cosCOD = 0.28 , par quel cosinus on déduit A'C' de AC?

Oui j'utilise la formule u*v= u*v*cos(u;v)
Mais je ne peut pas utiliser BD pour calculer A'C' avec la formule du cosinus, quel vecteur dois-je utiliser ?

chan79 a écrit:eh oui, ça marche

Merci. Dernière question , je dois calculer A'C'. Comment dois-je m'y prendre?

(AA') et (BD) sont perpendiculaires donc .... Ah oui donc ça fait: A'C'.BD = (A'A+ AC + CC').BD = A'A.BD + AC.BD + CC'.BD A'A.BD et CC'.BD étant égaux a 0 il ne reste plus que AC.BD égal a -7 comme on l'a démontré dans la question précédente. Donc A'C'.BD= -7 C'est ça ?

chan79 a écrit:en vecteurs:
A'C'=A'A+AC+CC'

Oui mais comment on fait avec A'A et CC' ?