Forum de Mathématiques: Maths-Forum

D'accord, je me suis corrigé je retrouve la même.
Merci beaucoup pour votre aide

Je trouve :
Z= (;) - x´)/-2
Y=(2y' -x´-;))/2
X= (-x´-2y'-3;))/2

Est ce bien ça ? Si c'est juste je ne vois pas comment en déduire p-1 !

Merci de votre aide

En fait j'ai d'abord calculé PX et après j'ai posé le système suivant :
x+y+4z=x'
x-y+2z=y'
x+y+z=z'

Est ce que ce système est juste ?

Bonjour à tous, Voilà je dois montrer que la matrice P est inversible et calculer P-1. Or une méthode est imposé je n'arrive donc plus a trouver P-1. Voici l'énoncé : Soit X= [x y z] X' = [x' y' z'] P =[1 1 4 , 1 -1 2 , 1 1 1 ] Il faut poser l'équation PX=X' et on est censé obtenir une et une seule...

J'ai reussie à m'avancer dans l'exercie mais je bloque sur la dernière question. Soit l=lim v_n . Quelle équation vérifie l ? Justifier que l>= 1 . Trouver l. Procéder de même pour w_n Je pense utiliser ce théorème : Si (v_n) est convergente et si lim v_n =l et si f continue en l, alors le n...

J'ai fais mes calculs avec cette fonction ! je pense qu'il y a que cette solution ! Merci

Manny06 a écrit:connais tu la fonction f ?

Justement la première partie s'agissait d'étudier la fonction f(x) = 2+lnx

Vous croyez que c'est cette fonction f ?

Bonjour à tous, Je bloque sur un exercice de suite. Voici l'énoncé : v_0=1 et w_0=5 et v_{n+1}=f(v_n) et w_{n+1}= f(w_n) Je dois indiquer sur un graphique les premiers termes de ces suites. Puis montrer que v_n est croissante et majorée par 4. Je pense que si je me débloque sur ce dé...

Merci beaucoup !

Mais maintenant je dois exprimer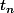 et 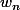en fonction de n.
Voilà ce que j'ai fais :




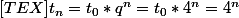
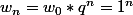
[/TEX]
Est-ce bien ça ?

Bonjour à tous, Voilà je viens de commencer le chapitre sur les suites et j'ai beaucoup de mal. Je bloque dès le début de l'exercice ! On a u_0=v_0=1 et u_{n+1} = 3u_n+2v_n et v_{n+1} = u_n+2v_n On pose : t_n = u_n+v_n et w_n=u_n-2v_n Et je doit exprimer t_{n+1} (rep w_{n+1} ) en fonction de t_n ( r...

merci beaucoup pour votre aide

Je comprends votre raisonnement, je cromprends pour n! mais par contre je ne comprends pas pourquoi vous dîtes c'est égal à 8! .

D8 étant juste un ensemble de distributions numéro 8 dans l'exercice mais ne représente pas un écolier ou autre.

Merci beaucoup

Bonjour à tous, Alors voilà, je n'arrive pas à résoudre un exercice de dénombrement... Voici l'énoncé: "On distribue n livres numérotés de 1 à n à p écoliers e1,e2,...,ep. On suppose p=n (quelconque) a) D8: chaque écolier à au moins un livre calculer card D8 b) quel est la probabilité pour que ...

L'initialisation j'ai compris et je l'ai faites ! Maintenant je comprends biens qu'il faut que je démontre pour n+1 mais je n'y arrive je me mélange les pinceaux ! Quand j'arrive à un résultat je ne sais pas si c'est terminé ! mais quand je regarde je me dis que comme n>1 et a positif je me dit que ...

Connais-tu le principe de récurrence ? Pour toi, c'est quoi ce principe ? Pour moi, il faut que j'arrive à montrer que Pn+1 est vraie soit que a*a^n>=a(1+n(a-1)) Si j'arrive à démontrer ça, ça veut dire que Pn est vraie ! Maintenant je ne comprend pas la démarche ! Je pars de a(1+n(a-1)) et j'essai...

Arony a écrit:n'oublie pas que toi doit arriver à n+1 pour que ça soit vrai

Pourquoi je dois arriver à n+1 ?
Je ne dois pas montrer que a^n+1 >= 1+(n+1)(a-1) ?

a^{n+1} =a* a^n donc comme a>0 en utilisant Pn: tu as a^{n} \geq 1+n(a-1) par hypothese de recurence tu multiples par a a*a^{n} \geq a(1+n(a-1)) tu obtiens donc a^{n+1} \geq a+n*a*(a-1) a+n*a*(a-1)=a+n(a^2-a)= a-1+1 + n(a^2-2a+1 +a-1)=1+(n...

arnaud32 a écrit:
donc comme a>0 en utilisant Pn

Je ne comprends pas ce que vous avez fait ! Je sais que a^n+1= a^n*a mais pour la suite ...

arnaud32 a écrit:tu peux proceder par recurence

Oui c'est ce que je dois faire ! Mais pour démontrer que Pn+1 est vraie je bloque ! et surtout je n'arrive pas à utiliser l'indication !

Bonjour à tous

Voila je dois démontrer a^n >= 1+n(a-1)

avec a appartenant a R+ et pour tous n dans N !
On me donne une indication, qui est : a²-2a+1=(a-1)²

J'ai reussi à démontrer que P1 est vraie mais je bloque pour Pn+1 et la suite !

Merci d'avance !