Par conséquent AM=AMA (en multipliant par A des deux cotés), ainsi toute matrice M de A(A) est dans B(A), on retrouve les condition de B(A) en multipliant par A donc A(A) inclus dans B(A)
Ca marche ?
67 résultats trouvés
Revenir à la recherche avancée
- 24 Sep 2015, 06:09
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
Ha c'est moi qui tourne autour du pot ? ...
Je ne sais pas comment faire, si je savais je ne serais pas venu ici.
Je ne demande pas qu'on m'apporte la réponse sur un plateau, simplement m'expliquer la méthode. Comment puis-je montrer que toute matrice M de du premier espace est dans le second ?
Je ne sais pas comment faire, si je savais je ne serais pas venu ici.
Je ne demande pas qu'on m'apporte la réponse sur un plateau, simplement m'expliquer la méthode. Comment puis-je montrer que toute matrice M de du premier espace est dans le second ?
- 23 Sep 2015, 22:03
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
- 23 Sep 2015, 19:57
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
Donc si je prends M la matrice nulle (appartenant à M3(R)), je montre qu'elle appartient au premier espace puis qu'elle appartient au second, cela me prouve l'inclusion ? ..
- 23 Sep 2015, 19:44
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
- 23 Sep 2015, 19:27
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
- 23 Sep 2015, 19:03
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
Espace vectoriel
Bonsoir, J'ai un petit doute sur un exercice. Soit A(M) et B(M) deux sous-espace vectoriel de M3(R) : M appartient à M3(R) tel que pour A(M) M=MA et pour B(M) AMA=AM Je dois montrer que A(M) est inclus dans B(M). Ca semble logique, mais je ne sais pas trop comment précéder pour être rigoureux. Je pe...
- 23 Sep 2015, 19:01
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 11
- Vues: 372
On a fait cet exemple en cours que je viens de retrouver .. Il faut à priori s'en servir
On a démontré que pour tout n supérieur ou égale à 2 :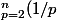 < ln(n) < \bigsum_{p=1}^{n-1} (1/p))
On a démontré que pour tout n supérieur ou égale à 2 :
- 16 Mar 2015, 20:53
- Forum: ✯✎ Supérieur
- Sujet: Suite convergente
- Réponses: 11
- Vues: 439
On va dire que c'est dans le cadre de révisions pour un DS sur limite, monotonie, continuité et dérivation .. Peut-être faut-il utiliser le théorème de la limite monotone, mais j'ai du mal à voir son application ici .. mais je crois que le prof à donner ça comme indication. En précisant bien qu'on n...
- 16 Mar 2015, 20:39
- Forum: ✯✎ Supérieur
- Sujet: Suite convergente
- Réponses: 11
- Vues: 439
Oui en ECE.
Je connais les intégrales mais je ne les ai pas encore étudiés cette année, donc je ne pense devoir résoudre cet exercice avec ....
Je connais les intégrales mais je ne les ai pas encore étudiés cette année, donc je ne pense devoir résoudre cet exercice avec ....
- 16 Mar 2015, 20:01
- Forum: ✯✎ Supérieur
- Sujet: Suite convergente
- Réponses: 11
- Vues: 439
- 16 Mar 2015, 19:28
- Forum: ✯✎ Supérieur
- Sujet: Suite convergente
- Réponses: 11
- Vues: 439
Suite convergente
Bonjour,
je dois démontrer que cette suite converge Un=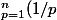 - ln(n))
Or je ne sais pas vraiment par où commencer ..
Merci d'avance
je dois démontrer que cette suite converge Un=
Or je ne sais pas vraiment par où commencer ..
Merci d'avance
- 16 Mar 2015, 19:21
- Forum: ✯✎ Supérieur
- Sujet: Suite convergente
- Réponses: 11
- Vues: 439
- 23 Déc 2014, 21:00
- Forum: ✯✎ Supérieur
- Sujet: Polynômes
- Réponses: 4
- Vues: 394
Polynômes
Bonjour, je bloque sur l'une des questions de mon exercice. Soit P(X) un polynôme de degré n et de coefficient dominant a_n Soit Q(X) = (X^2 -1)P'(X) - 2XP(X) On me demande de calculer le coefficient du terme de degré n+1 de Q(X), j'ai démontré avant que Q(X) était de degré inférieur ou égal à n+1, ...
- 23 Déc 2014, 20:16
- Forum: ✯✎ Supérieur
- Sujet: Polynômes
- Réponses: 4
- Vues: 394
La plus simple est la première. La plus ''pratique'' c'est tout aussi relatif, s'il s'agit simplement de remplacer a, b et c par des valeurs connues la 1ère reste la plus simple, s'il s'agit de démontrer la formule du delta la deuxième s'avère plus pratique. Tout dépend de ce qu'on veut en faire je ...
- 30 Nov 2014, 12:25
- Forum: ✯✎ Supérieur
- Sujet: Coefficient binomial
- Réponses: 5
- Vues: 398
D'accord merci beaucoup, je trouve cela bizarre quand même, car l'expression d'arrivée est bien plus compliquée que celle de départ, c'est ce qui m'a surement induit en erreur !
Merci à vous encore une fois ! Bon weekend :)
Merci à vous encore une fois ! Bon weekend :)
- 30 Nov 2014, 10:40
- Forum: ✯✎ Supérieur
- Sujet: Coefficient binomial
- Réponses: 5
- Vues: 398
Coefficient binomial
Bonjour, j'ai du mal avec quelques simplifications, notamment (p+1)parmi(n+1) - (p-1)parmi(n-1) .. je remplace avec la formule du binôme de Newton avec les factorielles mais je ne trouve rien de concluant
Merci de votre aide :)
Merci de votre aide :)
- 29 Nov 2014, 15:50
- Forum: ✯✎ Supérieur
- Sujet: Coefficient binomial
- Réponses: 5
- Vues: 398
- 06 Nov 2014, 20:57
- Forum: ✯✎ Supérieur
- Sujet: Théorème encadrement et somme
- Réponses: 7
- Vues: 471
J'ai trouvé  , est-ce juste ? Et je n'ai pas compris comment transposer cela en une suite géométrique ?
, est-ce juste ? Et je n'ai pas compris comment transposer cela en une suite géométrique ?
- 06 Nov 2014, 20:16
- Forum: ✯✎ Supérieur
- Sujet: Théorème encadrement et somme
- Réponses: 7
- Vues: 471
Non je n'ai pas vu ça, je suis en 1ere année ECE et je ne sais pas si c'est au programme.
Par contre j'ai oublié de donner une indication, car on a prouvé précédemment dans l'exercice l'inégalité suivante : - Pn(x) < \frac{x^{n+1}}{(n+1)!}e(x))
Par contre j'ai oublié de donner une indication, car on a prouvé précédemment dans l'exercice l'inégalité suivante :
- 06 Nov 2014, 19:37
- Forum: ✯✎ Supérieur
- Sujet: Théorème encadrement et somme
- Réponses: 7
- Vues: 471
- 67 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
