Forum de Mathématiques: Maths-Forum

J'ai un petit exercice (qui ne doit pas être très difficile) mais sur lequel je bloque... Je dois calculer l'erreur relative commise en estimant l'accroissement ;) f par la différentielle df dans le cas suivant: f(x,y)= xy , au point (x,y)=(2,3) avec ;)x = 0,1 et ;)y = 0,2 . La réponse (selon le re...

Sa Majesté a écrit:Non

Ok, tout semble logique maintenant
Ensuite, j'applique alors:

J'ai un petit exercice (qui ne doit pas être très difficile) mais sur lequel je bloque... Je dois calculer l'erreur relative commise en estimant l'accroissement ;) f par la différentielle df dans le cas suivant: f(x,y)= xy , au point (x,y)=(2,3) avec ;)x = 0,1 et ;)y = 0,2 . La réponse (selon le rec...

amine94 a écrit:Bonsoir
Factorise par a^(-1/n) et tu verras ce qui te reste

Il me reste:


Mais je n'arrive pas à voir comment obtenir alors le deuxième terme de mon produit dans ma réponse qui est:

Pourriez-vous m'aider à démontrer ceci, svp?




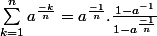
Un grand merci d'avance.

girdav a écrit:Tu applique la formule que tu connais pour au bon , étant fixé.

et tu l'appliques comment dans ce cas?

Pour a\neq 1 \sum_{k=1}^na^{\frac kn}=\frac{(a^{\frac 1n})^{n+1}-1}{a-1}-1=\frac{a\cdot a^{\frac 1n}-1-(a-1)}{a-1}=\frac a{a-1}(a^{\frac 1n}-1) . Au fait, je ne comprends pas ce passage: \sum_{k=1}^n a^{\frac {-k}{n}}=a^{\frac {-1}{n}} . \frac{1-a^{-1}}{1-a^{\frac {-1}{n}}} ...

Bonjour,

Je cherche une solution pour les deux sommes arithmétiques suivantes :





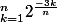
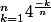
Un grand merci d'avance.