6 résultats trouvés
Revenir à la recherche avancée
- 27 Sep 2006, 19:58
- Forum: ✯✎ Supérieur
- Sujet: Inégalités (valeur absolue)
- Réponses: 11
- Vues: 3211
Pour l'inégalité triangulaire j'ai fait ca : Est ce que c'est bon aussi, et svp vérifier l'exercice 7 également. [CENTER] http://img97.imageshack.us/img97/7559/inexj0.gif [/CENTER] Avec votre methode oss007 : \large |a+b-c|=|a+b+(-c)|\le|a+b|+|-c| or : \large |a+b|\le |a|+|b| et \large |c|=|...
- 27 Sep 2006, 05:46
- Forum: ✯✎ Supérieur
- Sujet: Inégalités (valeur absolue)
- Réponses: 11
- Vues: 3211
allez des ptites idées svp J'ai une idéee pour 7, On a: \large |\frac{1}{1+x^2}-1|=\frac{x^2}{1+x^2} *Pour \large \underline{ x\neq0} 1+x^2>1 \qquad (1) \\ \alpha^2>x^2 \qquad (2) \\ (1)\times (2) = \alpha^2(1+x^2)>x^2 \Rightarrow |\frac{1}{x^2+1}-1|0 \Rightar...
- 27 Sep 2006, 00:37
- Forum: ✯✎ Supérieur
- Sujet: Inégalités (valeur absolue)
- Réponses: 11
- Vues: 3211
Salut,
Bon, j'ai séparé les question si ca peut vous aider, mais les questions peuvent être résolus indépendemment (d'après la prof).
Bon, j'ai séparé les question si ca peut vous aider, mais les questions peuvent être résolus indépendemment (d'après la prof).
- 26 Sep 2006, 23:36
- Forum: ✯✎ Supérieur
- Sujet: Inégalités (valeur absolue)
- Réponses: 11
- Vues: 3211
Re -
Les quelques idées que j'ai :
1. C'est l'inégalité triangulaire :
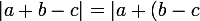|\le|a|+|b-c|)
Or :
Et donc :
Voila mon problème pour la première : je n'arrive pas à voir le lien ...
Les quelques idées que j'ai :
1. C'est l'inégalité triangulaire :
Or :
Et donc :
Voila mon problème pour la première : je n'arrive pas à voir le lien ...
- 26 Sep 2006, 21:49
- Forum: ✯✎ Supérieur
- Sujet: Inégalités (valeur absolue)
- Réponses: 11
- Vues: 3211
Inégalités (valeur absolue)
Bonjour, J'ai un DM à rendre dans les jours avenir et je bloque (complètement) sur quelques exercices. en fait, je ne vois pas comment partir ... 1. \large\forall (a,b,c)\in\mathbb{R}^3, |a+b-c|\le |a|+|b|+|c| 2. c'est fait, [center]*****[/center] 3. Montrer que \large \forall x \in \mathbb{...
- 26 Sep 2006, 21:33
- Forum: ✯✎ Supérieur
- Sujet: Inégalités (valeur absolue)
- Réponses: 11
- Vues: 3211
- 6 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
