Forum de Mathématiques: Maths-Forum

Doraki a écrit:Ca veut dire quoi, invariant par f ?
Si 0 < a < 1, que peux-tu dire de la mesure de l'ensemble [sqrt(a) ; a[ ?

Elle est nulle ???

Voici l'exercice de mon td
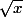
Soient f : x]0,1]-> et v la mesure de probabilité sur l'intervalle ]0,1] invariante par f.
Montrer que v est définie par v({1})=1 et v(]0,1[)=0
Pourriez vous me donner quelques piste pour démarrer?

Merci
Enfait je pense avoir réussi à faire les 2 sens

Bonjour, J'ai un exercice pour montrer qu'une application est ergodique par rapport à une mesure, mais je ne sais pas du tout comment attaquer: Soit n>1 un entiet et X=Z/nZ Soit P la mesure de probabilité sur X définie pas P({x})=1/n pour tout x dans X. Soient c dans Z et T:X->X donnée par T(a)=a+c ...