Forum de Mathématiques: Maths-Forum

yos a écrit:"au minimum" est de trop.


Si n=1, le 2ème cas ne peut pas se produire.

Ah oui, car si n=1
dim(H1) et dim(H2) sont 0!!
Merci

Ok j'ai compris pour le cas 1.
Oui je suis bete si n etait superieur a 0, on aurai un problème.

H1 a une dimension de n-1 et H2 a une dimension de n-1, dans le cas ou H1=!H2, on a au minimum une dimension de (n-1)+(n-1)-n=n-2
Or si n est inferieur a 2 on a un problème, c'est bien ça?
Merci

yos a écrit:Le premier cas est trivial mais il faut le signaler.


Ben non, ...

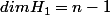
donc on a:

cas 1: dim H1=dim H2
Donc l'intersection est 0?

cas 2: dim H1=n-1
dim H2=n-1

Intersection n-(n-1+n-1)=-n + 2
?

C'est juste pourvu que H_1\neq H_2 . C'est la formule de Grassmann compte tenu du fait que H_1+H_2=\Lambda . Il faut écrire dim(\Lambda) et pas dim(n) . Il faut aussi pousser le calcul jusqu'au bout... Je pensais avor déjà poussé le calcul jusqu'au bout. Donc ici on a deux cas a étu...

La question est: Soit H1 et H2 deux hyperplans d’un ;)-espace vectoriel de dimension finie. Trouver la dimen- sion de H1 ;) H2 . J'ai trouvé Dim(H1 ;) H2 )=Dim(H1)+Dim(H2)-Dim(n) où n est la dimension du ;)-espace vectoriel. Est-ce vraie? Et si non, comment pourrais je résoudre correctement l'exerci...

Bonjour à tous! J'aimerais bien avoir un petit coup de pouce si possible avec cette question: Les séries de Fourier des fonctions réglées 2Pi–périodiques f peuvent être intégrées terme à terme. Ce-ci doit signifier que: Integral[de a à b] de f(x)dx= Somme[ck*Inteegrale[de a à b] de e^(ikx) dx] Mais...

Bonjour à tous! J'aimerais bien avoir un petit coup de pouce si possible avec cette question: Les séries de Fourier des fonctions réglées 2Pi–périodiques f peuvent être intégrées terme à terme. Ce-ci doit signifier que: Integral[de a à b] de f(x)dx= Somme[ck*Inteegrale[de a à b] de e^(ikx) dx] Mais ...

Bonjour,

Comment peut-on determiner la base du noyau de cette matrice?

1 2 1+2i 1-i
-1 3+i i 1
i -3-i -1 -1

merci!

Bonjours,
Pour la série du binôme, comment peut on montrer que:

(1+x)f'(x)=sf(x)

f(x) étant la limite de la série?

Merci

Ah c'est bon;)

Bonjour, J'ai essayé d'écrire la fonction factorielle avec un While et un For. J'ai écris le programme A et B, mais aucun des deux fonctionnent... Est-ce que quelqu'un peut les corriger? Merci (language Mathematica 7) Programme A 1 | n = 10; 2 | fact = 1; 3 | While[n > 1, 4 | n = n - 1; 5 | fact = f...

Tu sembles très mal connaître les objets que tu emploies, ça ne peut que compliquer la compréhension de l'exercice. V* ce n'est pas la transposée de f mais son dual, autrement dit, l'ensemble des formes linéaires de V. Une forme linéaire d'un K-ev V, c'est une application linéaire de V dans K. Donc...

Tu es sûr du vf(f(x))? Tu es sûr déjà que ça ait un sens? f, si j'ai bien compris l'énoncé (a priori il manque un bout) c'est une forme linéaire, donc par de V et est à valeurs dans un corps K. Donc f(x), c'est un élément de K. Du coup, ce serait quoi f(f(x))? Attention aux objets que tu manipules ...

Vu que f est linéaire on a:

f(x+f(x)v)=f(ax) ==> f(x)+vf(f(x))=af(x)
==> 1+vf(1)=a
C'est juste et si oui, que puis je en conclure?

Je ne vois pas où tu veut aller avec ça... Qu'est-ce que ça nous permet de calculer? Désolé pour toute ces questions..
Merciiii enormenent pour ton aide!!!

Ok donc quand f(x)=0
On a 1 comme valeur propre.

f(x)=(ax-x)/v
c'est ça se que tu voulais dire?

Ok je me suis mal exprimer.
J'ai trouver x+f(x)v=ax
a étant la valeur propre.
Mais je ne vois toujours pas les solutions évidentes.

a est une valeur propre de u si et seulement si:

il existe un x appartenant a un endomorphisme, avec x pas égale a 0.I telle que u(x)=ax

C'est ça, si oui comment je fais maintenant?
Merci pour ton aide!

Nightmare a écrit:Tout d'abord pour commencer, quelle est la définition d'une valeur propre? Donc que faut-il chercher?

Une fois ceci-dit, vois-tu des valeurs propres évidentes?

C'est l'ensemble des scalaire a tel que:

det(x+f(x)v-aI)
I étant la matrice identité.

Je ne vois rien d'évident...