Forum de Mathématiques: Maths-Forum

Je vous remercie sincèrement

Bonjour,
Soit D une partie de ,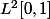
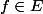On dit que D est dense dans si pour tout point il exicte une suite d'éléments de D qui converge vers
la question qui se pose c'est ""est-ce qu'on parle de la convergence au sens de ?""

MouLou a écrit:Salut. Ton ensemble ça reste bien une partie fermée bornée dans un espace de dimension finie non? (c'est inclus dans la boule que tu as donnée plus bas)

Oui il est inclus dans un fermé borné (compact) mais je pense qu'in n'est pas forcement compact.

Déjà ton ensemble est pas super clair. C'est quoi n ? à quoi ça sert de mettre un indice n à m_n ? Est-ce que t'es sûr des bornes de tes sommes ? Les éléments de ton ensembles sont des fonctions de quoi dans quoi ? Ensuite la compacité c'est une propriété d'un espace topologique. Là on a un ensembl...

Bonjour, On se place sur l'espace vectoriel E=L²([0,1]) des fonctions intégrables de [0,1] dans R muni de la norme ||f||=\Big(\int_0^1|f|^2\Big)^{1/2} . Dans cet espace, on considère des parties de la forme : U_n=\{f \in L^2[0,1]/f:x\mapsto \sum_{k=0}^{n}c_k\cos(2k\pi x)+d_k\sin(...

"" on peut trouver des élément de la réunion des Un aussi proche qu'on veut de n'importe quelle fonction f de L²([0,1]) "" c'est ça la définition de la densité d'un ensemble dans L² ? Oui, et pas que dans L² d'ailleurs : c'est la définition d'une partie "dense" dans n'...

Oui, et pas que dans L² d'ailleurs : c'est la définition d'une partie "dense" dans n'importe quel espace métrique... je vous remerci infiniment. je me demande est ce que l'ensemble reste compact si on le définie comme: U_n_k=\{f:x\mapsto \sum_{i=0}^{n_k} c_i\cos(2i\pi x)+d_i\sin&#...

MouLou a écrit:Salut, c'est quoi les x et y? des suites qcq? n'importe quelle suite?

salut,je vous remercie pour votre reponse
Les x et y sont des coefficients de Fourier par rapport a la fonction sinus et cosinus respectivement d'une autre fonction

MouLou a écrit:Salut, c'est quoi les x et y? des suites qcq? n'importe quelle suite?

salut,je vous remercie pour votre reponse


Les x et y sont des coefficients de Fourier par rapport a la fonction sinus et cosinus respectivement d'une autre fonction

bonjour, voilà je suis perdu a ce probleme, pourriez vous m'aider? On suppose que V est un opérateur et Vn est son estimateur c_{k,n},c_{k,0} les coefficients de Fourier par rapport a la fonction cosinus et d_{k,n},d_{k,0} les coefficients de Fourier par rapport a la fonction sinus de Vn et V repect...

Ben314 a écrit:Salut,
Tu prend n'importe quoi sur [0,1] (de norme <1), par exemple K(x)=x^2 et tu prolonge par périodicité...

prolengement par periodicité???

Bonjour, j'ai vraiment besoin d'aide s'il vous plait Je travaille sur un opérateur de Hilbert Schmidt à noyau de convolution défini par M(f)(t)=\int_{[0;1]} K(t-x)f(x)dx\ avec K\in L^2[0, 1] de norme inferieur strictement à 1 , et K périodique de période 1 . Alors, po...

Ben314 a écrit:Oui, et pas que dans L² d'ailleurs : c'est la définition d'une partie "dense" dans n'importe quel espace métrique...

je vous remerci infiniment.

Si f est une fonction quelconque de L²([0,1]), on peut toujours calculer les coeff. de fourriers an et bn de f et l'égalité de Parceval te dit que la norme (dans L²) de f, vérifie ||f||^2=\frac{1}{4}a_o^2+\frac{1}{2}\sum_{n\geq 1}(a_n^2+b_n^2) . Si pour tout n, on prend pour Pn le polynôme ...

Ben314 a écrit:Oui,
Il te suffit de considérer le polynôme trigo formé avec les coeff. de Fourrier d'indice <n et d'utiliser l'égalité de Parseval pour conclure que le reste est aussi petit que tu veut.

pouvez vous m'expliquer un peu plus[SIZE=5]??[/SIZE]

une autre question s'il vous plait,

est ce que la réunion des sur tout les est dense dans ??

Donc "ton" U_{n_k} c'est effectivement "mon" U(n_k,n_k) et, comme tout les U(?,?), il est compact car c'est la boule fermée de rayon n_k du s.e.v. de dim finie de L²([0,1]) engendré par les x\mapsto\cos(2 i\pi x) et x\mapsto\sin(2i\pi x) pour 0\leq i\leq ...

Salut, Je comprend pas trop tes notation (principalement ton nk : c'est UNE variable que tu note nk ? c'est bizare comme truc...) Ce que je crois comprendre de ton énoncé : 1) On se place sur l'espace vectoriel E=L²([0,1]) des fonctions intégrables de [0,1] dans R (ou dans C ?) muni de la norme ||f...

Salut, Je comprend pas trop tes notation (principalement ton nk : c'est UNE variable que tu note nk ? c'est bizare comme truc...) Ce que je crois comprendre de ton énoncé : 1) On se place sur l'espace vectoriel E=L²([0,1]) des fonctions intégrables de [0,1] dans R (ou dans C ?) muni de la norme ||f...

Je suppose que la norme sur L^2([0;1]) est N: f \mapsto \sqrt{\frac{1}{2}\int_{[0;1]} f^2} . Alors cet ensemble est l'intersection de P_{n_k} avec l'image réciproque de [0;n_k] par N^2 . La compacité d'une partie d'un evn ne dépend que de la partie et de la restriction de la norme à cette p...