Forum de Mathématiques: Maths-Forum

Ok merci !

Hmm ok mais je vois pas encore comment il choisit le n0, ce qu'il fait j'ai bien compris qu'il s'agit de la définition (enfin maintenant), mais je ne vois pas comment il fait pour choisir le n0.

Bonjour a tous, Dans un exercice on me demande de trouver l'infimum/supremum d'un suite donnée. Prenons par exemple : an = \frac{3n}{n+2} l'infimum c'est ok, par contre le supremum : le corrigé fait ceci : montre que an peut s'écrire : 3-\frac{6}{n+2} qu est donc 0, il faut trouver un no tel que ano...

Ah ! Je comprend de mieux en mieux ! a force de faire des dl autours de 0, j'en oublie presque que que c'est (x-a)^n et non x uniquement parce que a = 0 Pour ce qui est du corrigé quand il dit 1+X il sous entend que X = le dl de cos(x) sans le terme constant autours de 0. Pour ce qui est des limites...

Merci pour ta réponse, je vois beuaocup mieux le cheminement ! Pour vérifier si j'ai bien compris j'ai essayé un autre exemple : ln(cos(x)) J'ai donc développé cos(x) en 0 comme demandé dans l'énoncé: cos(x)=1-\frac{x^2}{2}+\frac{x^4}{24}.. Puis ln(u), si je résonne bien, u c...

Ok pour le premier, mais après je comprend pas pourquoi tu changes de point, et comment tu trouves le trouves le nouveau point ! Ensuite j'ai d'autres questions mais cette fois ci concernant les limites avec le développement limité. Comment faire les limites avec des développements limités ? exemple...

Peit-être parce que je vais devoir remplacer les u par le dl de sin(x) dans mon dl de 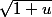? mais qu'estce que je fais du premier terme ? et si a la place de sin(x) j'aurai eu une autre fonction dont le dl aurait eu un premier terme constant différent de 0 ? quels sont les règles à suivre ?

Ok donc revenons au problème principal, la composition de dl ?

Ah oui en effet je devrais avoir u et non x.
De plus tu as encore raison,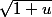 en 0 est égal à 1.

Je pense qu'il est correct maintenant ?

oups innatention il manque le terme en et la factorielle, ce qui donne
:

\sqrt{1+u} = 0 + \frac{1}{2\sqrt{1}}*x - \frac{1}{4} * 1^{-1/2} ... sin(x) = \sum_{k=0}^{oo} \frac{x^{2k+1}}{(2k+1)!} * (-1)^k Pour ce genre de développement limités ca va,, c'est surtout la composition, je vois pas comment faire vraiment, qu'estce que j'a ile droit de faire...

Bonjour, Je suis entrain de voir les développements limités. Pour les calculs de fonctions usuelles (exp, sin, cos...) je parviens à les faire. Cependant je ne vois pas complètement comment faire pour la composition de développements limités. Je ne sais pas ce que j'ai le droit de faire ? comment le...