Forum de Mathématiques: Maths-Forum

Jota Be a écrit:Oui c'est lourd mais il est nécessaire de donner une valeur exacte avant d'en donner une approximative.

Compris, en tout cas merci pour tout, merci de m'avoir aidé à réussir mon exercice ! :lol3:

Euh, tu veux plutôt dire que S' est négatif pour h\in]0;\frac{1}{\sqrt{8}}[ et est positif pour h\in]\frac{1}{\sqrt{8}};+\infty[ , non ? Et sinon, t'as vraiment bien arrondi ! Je préfère que tu gardes les valeurs exactes si possible. Euh oui, c'est S qui est décroissante puis croissante. :lol3: Le ...

OUh la boulette ! Heureusement que tu me le fais remarquer car je me suis tout à l'heure dit que j'allais le corriger mais je ne l'ai pas fait car j'ai une mémoire de poisson rouge. Il s'agit de \frac{1}{\sqrt{8}} ou -\frac{1}{\sqrt{8}} D'accord merci, j'avais trouvé également 1/racine de 8 :ptdr: ...

D'ailleurs ma soeur s'est trompée, ce n'est pas S= -\frac{0,3}{h^2}+2,4 mais S'= -\frac{0,3}{h^2}+2,4 . Ensuite, je trouve que la dérivée s'annule en h=\frac{1}{8} ou en -\frac{1}{8} . Comment arrivez-vous à trouver 1/8 ? Je persiste à trouver Racine de 8 ... Je résous l'équation -(0.3/h²) +2,4...

Bonjour, Quel trinôme ? Je n'en vois pas ici ! Ah oui pardon, en fait je suis obnubilé par le fait que mon prof de maths ne nous donne que des trinômes à étudier. Donc dans ce cas, la dérivée s'annule pour x=Racine de 8 ? Ou es-ce que je dois mettre le tout sur le même dénominateur et ainsi obtenir...

J'ai juste un petite question, la dérivée est bien un trinome, mais que vaut a ? -0,3/1 ?

Une surface n'est pas exprimée en mètres cube. Et je n'ai pas bien saisi ton résultat de S mais il ne me semble pas juste ! Nous avons bien S=2(1.20h)+2(Lh)+(1.20L) donc en remplaçant L par sa valeur en fonction de h, nous obtenons S=2,4h+\frac{0,3}{h}+\frac{1}{2} . Nous dér...

J'ai exprimé L en fonction de h, ce qui me donne L=\frac{0.3}{1.20h} Et ensuite pour la surface, sans le couvercle, je trouve : S=2(1.20h)+2(Lh)+(1.20L) Après avoir remplacé L par ce que j'ai trouvé précédemment et après avoir simplifié j'obtient ceci : S=\frac{h^{2}+5.20h+5....

Bonjour à tous. J'ai un petit soucis sur un exercice de mathématique. Voila mon problème : "Une entreprise doit réaliser des caisses en plastique sans couvercles de la forme d'un parallélépipède rectangle de volume intérieur 0.3 m cube. La longueur est fixée à 1.20m. Comment choisir la largeur L et ...

Fais une bonne figure tu comprendras, rappelles toi de ce que t'as vu en 4ème à propos des triangles rectangles Oh la la merci en effet avec la figure ça m'a sauté aux yeux ! Comment j'ai pu passer à côté de ça ... :dodo: Donc l²+L² = 10 L² = 10-l² A = lxL A² = l² x L² A² = l² x (10 - l²) A² = 10l²...

Manny06 a écrit:si l et L sont les côtés du rectangle
que vaut l²+L² ?
deduis en L² en fonction de l²
que vaut l'aire A du rectangle ?
exprime A² en fonction de l et etudie les variations de la fonction obtenue

En fait je ne vois pas ce que vaut l²+L². Vous ne voulez pas dire 2l + 2L ? Le périmètre ?

S'il vous plait ...

Bonsoir, j'ai un problème de mathématiques sur lequel je bloque. En voici l'énoncé : "C est un cercle de diamètre 10. Comment place t on les points ABCD sur le cercle de sorte que ABCD soit un rectangle d'aire maximale ?" Je ne sais pas du tout comment résoudre ce problème. Pouvez-vous m'aider ? :tr...

Pour la question 2), il faut que je trace la tangente au cercle E ? D'où le fait que le produit scalaire des vecteurs (MA+MB+MC) et des vecteurs (MA+MB) doit être égal à 0 ?

Carpate a écrit:Tu as donc :

= ...

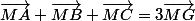
Merci, j'ai compris, au final, j'ai donc E un cercle de centre G et de Rayon 5.

Carpate a écrit:Chasles :

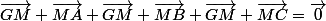
Oui mais je ne vois pas comment je pourrais définir un point M qui vérifie

Bonjour, j'ai un devoir de Maths dont l'énoncé est le suivant : "Soit ABC un triangle quelconque. Le centre de gravité du triangle ABC est le point G tel que : \vec{GA}+\vec{GB}+\vec{GC}=\vec{0} " 1) Determiner et constuire l'ensemble E des points M du plan tels que : Norme(\vec{MA}+\v...

st00pid_n00b a écrit:Il y a des angles qui se font remarquer car ils apparaissent souvent dans les problèmes de maths:
0; pi/6; pi/4; pi/3; pi/2; pi

Les autres angles font preuve d'un peu plus d'humilité.

D'accord, merci :lol3:

J'ai juste une petite question, c'est quoi au juste un angle remarquable ?

D'accord, merci beaucoup pour votre aide, je vais essayer de faire les autres, si j'ai un problème je vous tiens au courant :lol3: