376 résultats trouvés
Revenir à la recherche avancée
Taupin a écrit:Avec Tn le polynome de Tchebitcheff je suppose ?
oups, j'avais oublié de le mentionner.
C'est bien le polynome de tchebychev
- par bastien83
- 03 Fév 2008, 15:24
-
- Forum: ✯✎ Supérieur
- Sujet: cos/sin
- Réponses: 4
- Vues: 493
bonjour à tous,
je dois prouver que (1-x²)Tn''(x)-xTn'(x)+n²Tn(x)=0
je fais mon calcule et j'arrive à:
(x²n²)cos(nx)+(xn)sin(nx)=0
mais la je bloque . Si quelqu'un pouvait m'aider.
Merci d'avance
- par bastien83
- 03 Fév 2008, 15:12
-
- Forum: ✯✎ Supérieur
- Sujet: cos/sin
- Réponses: 4
- Vues: 493
Bonjour à tous, je travailles sur le polynome de tchebychev et j'ai deux petits . 1er: on me demande de calculer Tn(Chx)=? Moi jdis que ca fait ch(nx) mais ca me semble un peu simple dc..; 2eme: exprimer cos[(n+2)@)] en fonction de cos[(n+1)@] cosn@ et cos@ c'est du simple calcule trigo mais jtrouve...
- par bastien83
- 02 Fév 2008, 14:10
-
- Forum: ✯✎ Supérieur
- Sujet: petites questions
- Réponses: 3
- Vues: 807
bjr à tous et à toutes. J'ai un exercice à faire mais quelque chose me chagrine: on me demande de determiner les réels x solutions de l'equation cosnx=0 sachant que n >ou=1 je fais dc ceci: cosnx=0 Je pose X=nx cosX=0 ssi X=Pi/2 ou -Pi/2 dc nx= plus ou moins Pi/2 dc x= plus ou moins Pi/2n mais dans ...
- par bastien83
- 27 Jan 2008, 12:08
-
- Forum: ✯✎ Supérieur
- Sujet: verification
- Réponses: 3
- Vues: 620
bjr, j'ai une demo dans mon cours que je n'arrive pas à comprendre. Il s'agit de la demo suivante: l'image continue d'un segment est un segment. J'aurais voulu savoir si il existait un sit eou sont explique les demo de math sup et tout particulierement celle ci. Ou si quelq'un pouvait me l'expliquer...
- par bastien83
- 26 Jan 2008, 15:08
-
- Forum: ✯✎ Supérieur
- Sujet: demonstration
- Réponses: 3
- Vues: 457
merci à vous deux.
Mais est ce que l'un de vous peut me donner la demo car je ne l ai pas ds mon cours( :triste: ) et notre prof la mis ds la liste des questions pouvant tomber au concours blanc de demain.
- par bastien83
- 13 Jan 2008, 15:33
-
- Forum: ✯✎ Supérieur
- Sujet: theoreme
- Réponses: 3
- Vues: 513
bonjour,
je ne retrouve plus le resultat de l'image d'une suite convergente par une fonction continue.
Si quelqu'un pouvait me la donner (je ne demande pas la demo.)
Merci d'avance
- par bastien83
- 13 Jan 2008, 15:11
-
- Forum: ✯✎ Supérieur
- Sujet: theoreme
- Réponses: 3
- Vues: 513
yos a écrit:Ben non. Ta suite est définie par récurrence :
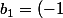^0(_0^0)b_0=1)
.
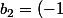^0(_0^1)b_0+(-1)^1(_1^1)b_1=0)
.
...
D'accord merci bien
- par bastien83
- 26 Déc 2007, 09:54
-
- Forum: ✯✎ Supérieur
- Sujet: suite
- Réponses: 7
- Vues: 741
yos a écrit: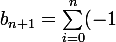^i (_i^n)b_{i})
.
Et c'est quoi ces questions?
les questions sont calculer les
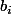
pour 0;1;2;3;4;5;6
montrer que
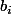
est rationnels
.....
Je penses donc avoir besoin d'une expresion de
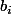
pour pouvoir y repondre.
- par bastien83
- 24 Déc 2007, 15:32
-
- Forum: ✯✎ Supérieur
- Sujet: suite
- Réponses: 7
- Vues: 741
bruce.ml a écrit:salut,
c'est b(i+1) ton sigma ? et (n,i) c'est le binomial ?
(n,i) est bien le binomila et sigma est la somme des i allant de 0 à n
dsl je metrise pas trop le tex.
- par bastien83
- 24 Déc 2007, 14:50
-
- Forum: ✯✎ Supérieur
- Sujet: suite
- Réponses: 7
- Vues: 741
bonjour,
Dans un exercie on me donne la suite suivante:

^i \times (n,i) \times b_{i})
cependant la majorite des question porte sur
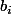
comment puis faire pour repondre à ces questions etant donne que
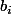
et dans la suite.
merci d'avance
- par bastien83
- 24 Déc 2007, 14:19
-
- Forum: ✯✎ Supérieur
- Sujet: suite
- Réponses: 7
- Vues: 741
donc si j ai bien compris les point d'inflexion sont les point ou y''/y'=0
c'est ca????
- par bastien83
- 09 Déc 2007, 18:53
-
- Forum: ✯✎ Supérieur
- Sujet: inflexions
- Réponses: 3
- Vues: 542
bonjour à tous et à toutes, j'ai un exo de math à faire mais je bloque un peu: l'equation est : y=(ahx)/(x^2+h^2) ou a et h sont sup à 0 j'ai fais sa derivée son tableau de var et son tracé.Mais maintenant on me demande de trouver les inflexions.Or je ne peux pas appliquer la formule habituelle . Ma...
- par bastien83
- 09 Déc 2007, 15:19
-
- Forum: ✯✎ Supérieur
- Sujet: inflexions
- Réponses: 3
- Vues: 542
Bonjour à tous, j'aurais aimer savoir qd je devais chercher les asymptotes et autres branches dans une etude de courbe parametrique. Par exemple pour l'etude de cette courbe: x(t)=4(1+t^2)/(1+t^2)^2 y(t)=8t/(1+t^2)^2 je trouve un tableau de variation sans "signe particuliers" c'est à dire sans valeu...
- par bastien83
- 02 Déc 2007, 14:51
-
- Forum: ✯✎ Supérieur
- Sujet: tangente,asymptote et branche parabolique
- Réponses: 1
- Vues: 954
bonjour,
j'aimerais savoir comment je dois faire pour passer d'une equation parametrique à polaire.
exemple d'equation:
x(t)=a(1+cos(t))
y(t)=asin(t)
j'ai voulu dire que
x=rô cos(@)
y=rô sin(@)
mais ca pas l'air de fonctionner à moins que je mis prennes mal.
merci d avance;
- par bastien83
- 01 Déc 2007, 17:00
-
- Forum: ✯✎ Supérieur
- Sujet: determiner une equation polaire
- Réponses: 2
- Vues: 2005
bonjour, j'ai une courbe parametrique def par: x(t)=4a(1-t^2)/(1+t^2)^2 y(t)=8at/(1+t^2)^2 ou a est un reel strictement possitif je dois etudié cette courbe. ca c'est fais. mais on me demande de determine tan 0(teta), la tangente de l angle polaire 0 du point M(t) en fonction de t . ET la ca bloque ...
- par bastien83
- 01 Déc 2007, 16:21
-
- Forum: ✯✎ Supérieur
- Sujet: courbe parametrique
- Réponses: 1
- Vues: 955
.