Forum de Mathématiques: Maths-Forum

Bonjour, j'ai la fonction f(x)= \frac{x^2+1}{\sqrt{x^2-1}} , et on me demande de trouver les asymptotes,si celles-ci existent. je n'ai eu aucun problème pour les asymptotes verticales, mais je ne parviens pas à trouver les asymptotes obliques. Lorsque je fais la limite en l'infini de f(x)/x ...

[img] [IMG]http://img338.imageshack.us/img338/8575/96313464.png[/img] [/IMG] Oui, si on choisit comme variable \alpha=\hat{BOE} , on trouve que le périmètre maximum est obtenu pour tan \alpha =2, ce qui donne une construction simple pour le résultat Perso, je trouve ça SUPER compliqué... Je peux bi...

Mais si le point E se trouvait de l'autre coté du point O, la largeur ne serait-elle pas égale à : "r-x" , ce qui changerait tous les calculs??

J'ai comme dérivée:



Après je trouve un maximum en

Donc pour avoir un périmètre maximum j'ai:

-

-

Vous pouvez vérifier svp??

Bah en posant x= [OE] et r= rayon j'ai :

largeur=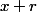

Le triangle BEO étant rectangle je peux affirmer que:

r²= [BE]²+x²
[BE]=

La longueur étant égale à 2 [BE]:

longueur=

et le périmètre =

Est-ce correct?

Bah, si on considère les points A et B comme étant les points de contact de la corde avec le cercle,C et D respectivement projections orthogonales de ces points sur la tangente et a= [AC] b= [AD] ===>a=b et c= longueur de la corde On peut alors dire que la périmètre du rectangle serait de: 2(a+c)=2(...

Non, je ne savais pas, je croyais qu'il s'agissait d'une simple parallèle...

Sinon, en gros je dois trouver la plus grande corde parallèle à la tangente pour déterminer le plus grand rectangle?

Bah j'ai tracé mon cercle, j'ai déterminé un point M dessus et j'ai tracé une tangente à ce cercle pour me représenter la situation.

Après j'ai tracé ma parallèle mais je ne vois aucun rectangle... je crois qu'il y a une erreur dans la compréhension de l'énoncé...

Bonjour, j'ai un exercice de dérivée à faire mais le problème est que je ne comprends même pas l'exercice... Voici l'énoncé: " On considère une circonférence de rayon r et sa tangente au point M. En menant une corde parallèle à cette tangente, on construit un rectangle ABCD. Parmi la famille des rec...

Ok, merci je crois avoir trouvé la réponse mais bon, avec la fatigue je vérifierais demain :D

Merci en tout cas ;)

Voilà, J'ai un système d'équations trigonométriques à résoudre. Le problème est que je n'ai jamais eu à résoudre de tels problèmes et donc, je n'ai aucun idée de la démarche à suivre. Je tourne en rond depuis un moment sans jamais avoir réellement trouvé de vraies pistes. Voici l'énoncé: Déterminer ...

je devrais avoir 2 raisonnements? L'un pour x >= à 1 et un autre pour x<1 ??

Bonjour, excusez-moi mais il y a quelques inéquations d'un travail que je n'arrive pas à résoudre, j'espérais que vous puissiez me donner un coup de main. Voici l'une d'entre elles: V(x²-1) - V(x.(x-1)) > x-1 (V = racine carrée, je n'ai pas réussi à incorporer le symbole) Merci de votre aide.

Le problème est que tu me proposes une solution graphique du problème, hors j'ai besoin d'une solution algébrique, et c'est justement là que je coince :s
Enfin pour m différent de 0 puisque, la solution de m=o est, si j'ai bien compris, l'ensemble des réels négatifs.

Excusez-moi, je dois définir ce système, m étant un paramètre réel

x < ou égal à m

m²2.x+2 > ou égal a 3m

Excusez-moi, je dois définir ce système, m étant un paramètre réel

Mais il doit y avoir plusieurs x étant donné que l'énoncé est au pluriel...

En toute logique, c'est l'aire de la base multiplié par la hauteur, donc je dirais:

V = ;) x R² x h

Voilà, j'ai un exercice sur lequel je n'ai pas trop le temps de me pencher, c'est pourquoi je viens demander votre aide afin de me donner des pistes de résolution. On a un cylindre de longueur L et diamètre ;) (phi). On doit trouver les valeurs de x dont il faut diminuer la longueur et augmenter le ...

Je me disais bien aussi. Sinon Low Geek, je pense avoir trouvé ton erreur. le reste est tout le temps 1 degré inférieur aux diviseur. Hors le plus haut degré du diviseur est "x²" donc le reste a un degré en x et n'est donc pas constant. On peut écrire: R=cx+d Et à ce moment là, on commence l'identif...