Forum de Mathématiques: Maths-Forum

Bonjour,

Pouvez-vous m'expliquer comment fait-on pour passer de ca :



à ça :



En vous remerciant par avance.

Merci, probablement la raison pour laquelle le y a été omis

Bonjour, Voici un extrait de mon cours de proba : Grâce au changement de variables y = \lambda x, E(X) = \bigint_{0}^{+00} x\lambda{e^{-\lambda x}}dx = 1/\lambda \bigint_{0}^{+00} {e^{-y}}dy Je ne comprends pas comment on arrive à ce résultat, car je n'obtiens pas le même. Pouvez-vous me dé...

Problème résolu merci

Matt_01 a écrit:Tu confondrais pas avec la notion de langage reconnaissable/rationnel ? Dans ce cas le lemme de l'étoile est simple à appliquer.

Je connais le lemme de l'étoile, mais je ne vois pas comment l'appliquer pour démontrer qu'un langage n'est pas reconnaissable

Pour moi cet ensemble est trivialement démontrable. En effet, tout élément de cet ensemble est de la forme (ab)^n, où ab est donné, donc peut être indexé par n. Si c'est a^nb^p , c'est encore démontrable car chaque élément peut être indexé par un couple d'entiers, et on sait que NxN est démontrable...

Si (a,b) \in \mathbb{N}^2_{*} , la propriété est vraie par le théorème de Cantor à \mathcal{P}(N)=2^{\mathrm{card}\,N} car: card(N) \lt \mathrm{card}\mathcal{P}(N) As-tu une explication de pourquoi { a^{n}b^{p} tel que n et p appartient à N} est dénombrable alors que...

nodjim a écrit:Aucune indication sur a et b ?

Si tu veux pour n = 2 on a le mot aabb, pour n = 3 aaabbb, peu importe la valeur de a et de b

On peut faire la meme chose pour 1 et 0 : 10 1100 111000 ....

ps: a et b ne peuvent représenter que des chiffres, c'était peut etre ce que tu te demandais

Bonjour,

Pouvez-vous m'indiquer pourquoi l'ensemble suivant n'est pas dénombrable ?

{ tel que n appartient à N}

J'ai énormément de mal avec cette notion.

En vous remerciant par avance.

Bonjour, Voici ce que dit une correction : A(0) = 1 A(1) = 1 A(n) = A(n-1) + A(n-2) + 1 On a donc A(n) = 2 Fib(n) - 1. Bien que ce soit vrai, je n'arrive pas à comprendre comment peut-on deviner aussi simplement que A(n) était égal à 2 Fib(n) - 1. Bien sur on sait que Fib (n) = Fib(n-1) + Fib(n-2) m...

Bonjour, Voici une partie de mon cours : " 1.2 Variables aléatoires réelles discrètes (fi nies) Définition 1.6 : Soit E une partie finie de R. Une variable aléatoire réelle discrète, que l'on notera dans toute la suite v.a.d., est une fonction X : X : ;) --> E w --> X(w) = x. On dit que x est u...

Bonjour,

Je n'arrive pas très bien à comprendre la définition de la limite avec l'utilisation de Epsilon. Si quelqu'un pouvait m'expliquer cela de façon précise ou me donner un lien qui mène à une explication claire avec illustrations.

Merci d'avance

y6227 a écrit:In cependant ne vaut pas In non ?

Ah oui OK c'est bon merci! je pensais qu'il fallait prouver que c'était égale à d'où mon incompréhension.

Dinozzo13 a écrit:Salut !

Que vaut ?

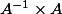
In cependant ne vaut pas In non ?

Bonjour, L'exercice consiste à démontrer ceci : (ABA^{-1})^3 = AB^3A^{-1} A et B étant des matrices de taille n * n inversibles. je ne comprends pas la correction qui est celle ci : (ABA^{-1})^3 = ABA^{-1} ABA^{-1} ABA^{-1} = AB^3A^{-1} En effet, je dois donc comprendre que (A^{-...

Bonsoir, Voici un extrait du cours : On considère une équation de la forme ax^2 + bx + c \equiv 0 [p] où p est premier; On suppose que a n'est pas congru à 0 modulo p; dans le cas contraire l'équation est de degré au plus 1. Si p=2 il suffit de regarder si 0 et 1 sont racines modulo 2. Supposons mai...

vincentroumezy a écrit:Bonsoir.
Appliques l'algo d'Euclide.

Merci! As-tu une idée pour la deuxième question ?
Cordialement

Bonjour, Comment dois-je procéder pour trouver deux entiers relatifs u et v tels que 2873u + 1001v = 13 sachant que le pgcd de 2873 et 1001 est 13. J'ai donc simplifié par 221u + 71v = 1. Comment dois-je également procéder pour savoir s'il existe deux entiers relatifs u et v tels que 2873u + 1001v =...

Bonjour et bonne année, Voici l'énoncé d'un exercice: Connaissant le reste de la division euclidienne d'un entier par 10, pouvez-vous en déduire celui de la division euclidienne de cet entier par 5? par 6? Intuitivement je sais résoudre l'exercice mais je ne comprends pas très bien la correction du ...

Bonjour, Voici la question d'un exercice : Soient E et F deux ensembles et f une application E -> F. Démontrer que : \forall A,B \in P(F) f^{-1}({A}\cap{B}) = f^{-1}(A) \cap f^{-1}(B) Voici la correction du professeur: x\in{f^{-1}({A}\cap{B})}\Leftrightarrow f...