Forum de Mathématiques: Maths-Forum

J'ai finalement trouvé la solution, je vais la poster pour ceux qui sont intéressés:



Et il suffit de tendre vers l'infini...

Non j'ai pas d'indication. C'est un exercice d'oral de mines je pense.

Personne n'a une piste?

zygomatique a écrit:salut

où intervient a dans la définition de u_n ?

Oui excuse moi,

Bonjour tout le monde, depuis quelques jours je sèche sur un exercice sur le séries et j'aimerai bien avoir une indication :) Soit a>0 et u_{n+1}=ln(\frac{e^{u_n}-1}{u_n}) on pose v_n=\prod_{k=0}^{n}u_k Il faut montrer que u_n tend vers 0, ça je l'ai fait, mais je n'ai pas réussi à montrer q...

Bonjour, Il doit encore manquer quelque chose au sujet de A parce que si A est nulle par exemple, l'énoncé est faux, vu que la relation donne 0=0 et M=M (selon si P a un coefficient constant ou non), qui n'implique pas grand chose sur M.. Damien Bonjour, excusez moi j'ai oublié une autre condition:...

Bonsoir; Ne faut-il pas supposer que A est inversible (au moins) ? Si ce n'est pas le cas, alors P(0)=0 car 0 est valeur propre, donc P = X.Q et P(-A) = (-A).Q(-A) = -Q(-A).A a au moins autant de noyau que A ... En fait, le problème initiale c'est: soit A matrice réelle et M matrice symétrique réel...

Bonsoir,
Soit une matrice réelle et son polynôme minimale, je veux montrer que est inversible. Quelqu'un a une piste?
Merci

Bonjour, soit
avec dans .
Je voudrais savoir si le minimum de f sur est fini ou pas.
Merci

Bonjour, si p est un projecteur orthogonal on peut affirmer qu'il est borné (car sa norme triple est majoré par 1). Mais je cherche un exemple de projecteur (à fortiori non orthogonal) qui n'est pas borné.
Merci.

Je voulais poster la réponse depuis longtemps mais là voici :we:
j'ai majoré par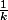 puis par et on montre que

Sourire_banane a écrit:Salut,

Tu peux trouver un équivalent de la somme (indexée par p) des 1/k² lorsque p devient grand.
Essaie une comparaison série-intégrale.

oui j'ai fait une comparaison série- intégrale pour montrer que cette somme est majoré par 1/n, en fait on a même équivalence

bonsoir, je dois montrer que \sum_{k=n+1}^{\propto }\frac{1}{k(k+1)}\int_{0}^{1}\frac{x(1-x)}{k+x}dx\leq \frac{1}{12n(n+1)} j'ai majoré \frac{1}{k+x} par \frac{1}{k} , et \frac{1}{k^2(k+1)}=\frac{1}{k+1}-\frac{1}{k}+\frac{1}{k^2} , la premiere somme est télescopique e...

Bonsoir,
Je voudrais montrer que l'ensemble A des fonctions f:[0,1]-R de classe 1 tel que f(0)=0 n'est pas un fermé pour la norme infinie.
Je dois donc trouver une suite f_n qui converge uniformement vers f qui n'est pas de classe 1. Des idées? Merci.

Merci tout le monde pour vos conseils, en effet j'avais commencé à faire des annales de l'X, pour l'instant ça marche super bien, je suis parmi les 5 premiers, c'est bien mais je veux aller plus loin, genre être dans les 2 premiers mais j'arrive pas à le réaliser. Quelque idées? Conseils? Merci infi...

Skullkid a écrit:Oui, ou plus simplement fn(x) = 1 si x est dans E, 0 sinon. L'énoncé que tu as donné ne demande pas que les fn soient continues par morceaux.

Mais je crois que pour intégrer f, il faut qu'elle soit continue par morceaux

si dans
sinon
mais cette fonction n'est même pas continue par morceaux

cuati a écrit:Bonjour,
une autre idée : découper [0,1] en des intervalles de plus en plus petits.
avec

C'est ce que j'ai essayé de faire au début, et je ne comprend pas très bien ta fonction

Skullkid a écrit:Bonjour, déjà est-ce que tu me donner un ensemble dense dans [0,1] ?

J'ai pensé à , mais je vois pas le rapport

bonjour,j'ai un peu du mal sur cet exo qui n'est pas évident (je voudrais qu'un indice):

Construire telle que et
l'ensemble des tel que ne tend pas vers est dense dans

merci