Forum de Mathématiques: Maths-Forum

Pour trouver une UNIQUE solution, c'est le théorème de bijection, qui > est ce que la fonction est strictement croissante ou strictement décroissante (cad monotone), de l'intervalle [0,1] à l'intervalle image .... > si oui, alors la fonction admet une bijection de [0;1] vers l'intervalle image .......

Bonsoir, Je dois montrer que f(x)=0 a une unique solution sur [0;1] On sait que f:x->e^x+x-2 Je sais qu'on doit faire le Théorème des valeurs intermédiaires mais je ne l'ai jamais vraiment appliqué donc je ne saurai comment répondre a cela.. A part dire : Pour avoir f(x)=0 sur l'intervalle [...

Une aide quelqu'un ?

Qu'est-ce que la TVI
Tu peux me detailler un peu ton raisonnement s'il te plait ? Merci d'avance.

f(0) = 6 ca m'aide pas plus que ca... :/

c'est 5,22 environ mais quelle est la methode a utiliser?

Bonjour


Je n'arrive pas a resoudre cette equation :



J'ai eassye de factoriser, sans succes, je n'ai pas la methode, toute aide sera grandement appréciée.

Bonjour a tous, J'ai qq problemes, toute aide sera appréciée : f(x) = x^3-5x^2-6 Limite (+oo) f(x) = Lim x^3 = +oo Limite (-oo) f(x) = Lim x^3 = -oo Derivee ? f'(x) = 3 \times x^2-2 \times 5 \times x^1=3x^2-10x Tableau de signe/Variation ? x | -oo |0| +oo 3x^2 | - | + -10x | + | - f'(x) ...

Quand j'utilise x_mm' et y_mm c'est pour faire le produit scalaire et montrer l'orthogonalité des vecteurs. Enfin bref, j'ai fini l'exo, je reviendrai avec la correction si tu veux ? (Ça sera une feuille manuscrite du prof, je la scannerai).

Merci quand même tu m'as bien aidé.

J'ai reussi la 2) En fait il fallait dire que (AM) etait perpendiculaire a (MM') pour que M, ou qu'il soit, on a (AM)//(BM') pour calculer l'affixe du vecteur MM' j'ai fait z'-z pour arriver a (4ixy-8iy-4y^2)/(x^2+y^2-4x+4) J'ai ensuite demande a un camarade ce qu'il avait fait, il me dit qu'il s'es...

Pour la construction c'est simple, M d'affixe z est le symétrique de M' d'affixe z' par rapport a l'axe des abscisse. M peut être partout sauf sur A. - "Réaliser une figure pour le point Q d'affixe 3-2i" Donc le point Q a pour coordonnées (3; -2) et faut placer M dessus ? Pas sur de comprendre ..

Ça doit être un DM tiré d'internet ou d'un livre alors...

Donc faut faire si l'affixe de A et l'affixe de B sont des réels alors (z'-a)/(z-b) sera toujours un réel ?

Oui en effet, j'avais oublier cette méthode la ! Qui est pourtant dans les bases... \vec{AM} = \vec{BM'}\times k k etant un nombre reel. Alors, les deux vecteurs sont colinéaires et donc parallèles. Pour la 2) "Generaliser les resultats de la question 1)c." dire que AM = k*BM' c'est de...

Je vois pas en quoi dire que

Affixe de AM = z - 2
et Affixe de BM' = + 2

va démontrer quoi que ce soit ... dsl de ne pas voir la demonstration que je devrais emprunter

Affixe de c'est
Affixe de c'est

Faudrait faire
Mais j'y arrive pas avec ses lettres.

Affixe de A c'est 2
Affixe de B c'est -2
Affixe de M c'est ??
Affixe de M' c'est ??


Affixe de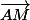 c'est
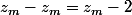
Affixe de c'est

Comment fait-on pour la c) ???

Faut montrer qu'ils sont colinéaires j'imagine ?

Mais pour les coordonnées de M et M' on met quoi ? xm ym et xm' ym' ? Mais z=z' donc M=M' ?
Donc M est sur la droite (AB) ?

Quelqu'un?

z'=

Dans je dois remplacer par (x+iy) et (x-iy) ?

Donc pour la b, je fais comment ?