Forum de Mathématiques: Maths-Forum

Salut,
j'ai revue ma copie, mais je ne trouve pas comme toi. En posant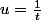 , et après le DL en 0, j'ai . En revenant à la variable d'origine et avec le critère de Riemann, je peux conclure que l'intégrale converge...non?

Bonsoir Iaya,
J'ai fais un changement de variable pour les DL. J'ai posé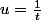 avec ... si c'est ce que tu veux dire (sinon, je n'est pas compris ta phrase... :euh: )

Bonjour, je souhaiterais un petit coup de pouce pour un problème : Soit f(t)=\frac{\tan^{-1} t}{t}-\frac{\pi }{2(1-t)} une fonction définie sur )0;+\infty ( 1) montrer que f est prolongeable par continuité en 0 \Rightarrow Ok, j'ai trouver que f est prolongeable en posant f&#...

Je me suis encore planté... :mur: ... j'ai trouvé ma relation entre et ...

Par contre, pour l' ex2, quand je calcule , j'arrive à :
je suis pas loin d'avoir en fonction de à la puissance près... si quelqu'un à un tuyau...

merci pour vos indications! Si je ne me suis pas planter dans le développement de ; je retombe bien sur l'égalité de départ.
Merci à tous les deux!

Bonjour Mathelot, Pour le changement de variable, je ne vois pas trop où tu veux en venir : si je pose u=a+b-x , j'ai du=-dx donc -du=dx , ok. Les bornes de l'intégrale deviennent : si x=a, u=b et si x=b, u=a. De plus j'ai x=a+b-u. Mon intégrale devient : \int_{b}^{a}{-(a+b-u) f(u)du...

j'ai rien dit.... je l'ai la puissance 3/2! :id:
merci.

Merci pour ton aide, mais ce serait plutôt puissance 1/2 pour oter la racine, non?

Bonjour à tous, J'ai des exercices sur les intégrales qui sont un peu corsés... j'aimerais un coup de main pour me lancer sur le chemin de la solution! Ex1 Soit f une fonction continue sur [a;b] tel que ;) x ;) [a;b] , f(x)=f(a+b-x) 1) montrer que l'on à l'intégrale de a à b (x f(x) dx) = (a+b/2) in...