Forum de Mathématiques: Maths-Forum

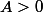
deltab a écrit:C'est plutôt et et non et

salut, la limite en (-infini), et pour les notation vous êtes libre, A , B, epsilon, delta...., mais le sens de de définition qu'est important.

Salut,j'ai une petite question,
comment on montre avec la définition (epsilon, delta) de la limite que la fonction x(carré)+1/x-1 tend vers -infini quand x tend vers - infini.
merci et dsl. pour la mauvaise écriture.

Judoboy a écrit:Non je donnais un contre exemple, on a une boule de centre 0 de rayon >0 (pour la topo L-infini) qui est incluse dans ton ensemble donc il n'est pas d'intérieur vide.

Merci, pour moi aussi, c m apparaitre très bizarre cette proposition, je la trouve dans un livre d'optimisation.

Judoboy a écrit:Si ton ouvert a une mesure M, la boule de centre 0 de rayon 1/M de L infini est incluse dans la boule unité de L2.

Tu veut dire que la boule unité de L2 contient un élément de L-infini, qui est la fonction caractéristique correspond à la boule de centre 0 et de rayon 1/M. c ça?

girdav a écrit:Tu te places dans quel espace mesuré ?

un ouvert de Rn, muni de la tribu de Borel.

Salut
j'ai besoin d'une démonstration du lemme suivant,
la boule unité de l'espace L2 est d'intérieur vide par apport a la topologie de L-infini.

salut à tous
Comment je peut montrer que la boule unité de L2 est d'intérieur vide par apport a la topologie de l'espace L-infini .

barbu23 a écrit:Bonsoir,
Tu as
Quelle sont les normes que tu affectes à chacune des et ?
, mais dans , non ?
J'ai du mal à comprendre l'expression de . :doh:

La norme Lp,

salut
Soit A un opérateur d'un espace de Banach Y vers Y' ( dual de Y), tel que A est définie par: Ay=(|y|^{p})y, p est positive.
comment calculer la dérivée de A.

salut, 1) Dans la théorie de contrôle optimal on utilise toujours l'équation l'équation adjoint pour déterminer les conditions d'optimalité de notre système, on sait qu'on peut introduire l'état adjoint comme un multiplicateur de Lagrange, est-ce que il y a d'autre méthodes pour qu'on obtient l'équa...

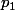
[quote="Rifl3"]Je n'ai pas trop compris ta réponse, cela définit un ouvert mais pas sur ?? :/[/QUOT
salut
pour le 4 ème question il suffit d'utilise la négation de la définition de- deux norme équivalentes-, vous devez travailler avec des inégalité.

chan79 a écrit:la fonction que je t'ai proposée est continue en 0 et seulement en 0

merci, c'est le bon et le simple exemple.

salut un petit exemple f est définie de la façon suivante si x est rationnel, f(x)=0 si x est irrationnel, f(x)=x cette fonction f n'est continue qu'en 0 cette fonction n'est pas continue en aucun point!, vous pouvez me donne une fonction qui est nul part continue sauf en un point? c'est ça le cont...

ev85 a écrit:Non, il n'y a aucune raison.

merci, vous pouvez me donner un contre exemple?

ev85 a écrit:Oui.

Ce sont des notions locales. Je ne sais pas ce que veut dire ponctuel. Le contraire de local est global.

salut, je veux dire , si une fonction est continue en un point, e s q, il existe tjr un voisinage de ce point, tel que cette fonction soit continue sur tout ce voisinage.

salut
on peut avoir une fonction qui est continue juste en un seul point?
même question pour la dérivabilité?
d'une autre manière, la continuité ( la dérivabilité ) sont des notion ponctuels ou bien locals?

salut
je besoin d'un petit programme sur matlab pour la méthode de Newton à une pas de recherche.

la norme est une application continue, ( la valeur absolu est une cas particulier), est la composition de deux applications continues est une application continue.

bonjour,
comment on peut généraliser la mèthode de Newton pour l'equation F(x)=0, s'achant que F est non différentiable et elle est définie sur un espace de Banach vers un autre espace de Banach.

salut,
Il y a un théorème qui dit ; X est un espace de Banach de dimension finie ssi la boule unité est compacte.
c'est le théorème Reitz. donc cette ensemble ne peut pas etre compacte.