28 résultats trouvés
Revenir à la recherche avancée
un fin de question bizarre!!!
j'ai démontrer que: B + B^(-1) = A + A^(-1) Avec A un générateur des racines n-ièmes de l'unité... On me demande: en déduire que B = A^(-1) ou B = A Ce n'est pas difficile a en avoir l'intuition mais je n'arrive pas a le démontrer rigoureusement... Merci pour vos remarques et pour vos pistes
- 28 Nov 2009, 16:44
- Forum: ✯✎ Supérieur
- Sujet: un fin de question bizarre!!!
- Réponses: 5
- Vues: 646
- 06 Fév 2007, 21:56
- Forum: ✯✎ Supérieur
- Sujet: polynome
- Réponses: 10
- Vues: 1109
- 06 Fév 2007, 21:50
- Forum: ✯✎ Supérieur
- Sujet: polynome
- Réponses: 10
- Vues: 1109
P(x) = 16x^{5} -20x^{3} +5x -1 en fait le but est de le factoriser sur R et C en sachant qu'il possède une racine double... donc ( P(a)=0 et P'(a)=0 ) Je trouve plusieurs factorisation... 1) P(x) = \frac{(x-1)(4x + \sqrt{5} +1)^2(4x - \sqrt{5}...
- 06 Fév 2007, 21:40
- Forum: ✯✎ Supérieur
- Sujet: polynome
- Réponses: 10
- Vues: 1109
polynome
Une petite question sur les polynome a factoriser: En effet je voulais savoir pour factoriser un polynome du degré 5 sur C (complexe) 16x^{5} -20 x^{3} +5x -1 , il ya til une méthode précise (bien entendu non ^^) , alors faut il le factoriser sur R puis sur C ou faut t il faire autrement... (Pas de ...
- 06 Fév 2007, 21:26
- Forum: ✯✎ Supérieur
- Sujet: polynome
- Réponses: 10
- Vues: 1109
- 06 Fév 2007, 20:14
- Forum: ✯✎ Supérieur
- Sujet: Algèbre
- Réponses: 2
- Vues: 480
Algèbre
Bonjour, On définit A={ a + bj | a,b \in Z} ou j = e^{\frac{2i\pi}{3}} Montrer que A est un sous anneau de C (complexe): Jarrive a démontrer la stabilite de laddition , de lopposé mais pas de la multiplication... J'arrive à: (a+bj)(c+dj)=ac + j(bc + ad) + j^{2}(bd) Co...
- 06 Fév 2007, 19:04
- Forum: ✯✎ Supérieur
- Sujet: Algèbre
- Réponses: 2
- Vues: 480
- 15 Jan 2007, 23:56
- Forum: ✯✎ Supérieur
- Sujet: Decomposer en élément simple...
- Réponses: 3
- Vues: 810
Decomposer en élément simple...
Bonjour , voila dans un exo je dois tout d'abord decomposer une fonction en élément simple cependant dans un de ces termes x^7 +1 je n'arrive pas a le factoriser... Si cela peut vous aider , la fonction est \frac{x^7+1}{x^2+1} Je voudrais savoir seulement si on peut factoriser x^7 +1 , sinon je voud...
- 15 Jan 2007, 22:45
- Forum: ✯✎ Supérieur
- Sujet: Decomposer en élément simple...
- Réponses: 3
- Vues: 810
Limite...
Pouvez vous m'aider pour trouver la limite de Vn quand n tend vers + infini
Vn= nln(a) - ln(n)
Merci bcp je gère pâs trop la manipulation du Ln!
Vn= nln(a) - ln(n)
Merci bcp je gère pâs trop la manipulation du Ln!
- 12 Déc 2006, 15:47
- Forum: ✯✎ Supérieur
- Sujet: Limite...
- Réponses: 3
- Vues: 558
Logique...
Bonjour voilà une simple question, pour certains mais j'ai quand même un doute.......
Si est vrai
est vrai
et si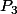 ===>
===> P_5) est vrai
est vrai
Est ce qu'on peut dire queP_5) est vrai???
est vrai???
Merci bcp !!!!
Bonne soirée
Si
et si
Est ce qu'on peut dire que
Merci bcp !!!!
Bonne soirée
- 28 Nov 2006, 18:43
- Forum: ✯✎ Supérieur
- Sujet: Logique...
- Réponses: 2
- Vues: 466
Vrai ou Faux...
Bonjour je vien de calculer la limite quand x tend vers O de :
}{tan(x)^2})
Je trouve 2 sa vous parez bon???
Merci fonfon:)
Je trouve 2 sa vous parez bon???
Merci fonfon:)
- 13 Nov 2006, 18:59
- Forum: ✯✎ Supérieur
- Sujet: Vrai ou Faux...
- Réponses: 1
- Vues: 559
Je ne comprend pas pour l'exercice 1 ...c'est quoi f(L)? Et pour l'exercice 2 le module de \frac{-2}{i} c'est 2 et l'argument de \frac{-2}{i} c'est \frac{\pi}{2} ?? C'est sa?? Et tu a une idée sur trouver les solution de (E) Pour les u^5=1 j'ai trouvé: u_{1}=1; u_2=e^{\frac{2i\pi}{5}};u_3=e^{\frac{4...
- 12 Nov 2006, 22:53
- Forum: ✯✎ Supérieur
- Sujet: Convergence...
- Réponses: 3
- Vues: 566
Convergence...
Bonjour voilà j'ai un DM a rendre demain j'ai cherché jusqu'a ce soir , mais des questions reste sans réponses alors j'ai quand même répondu , mais je ne sais pas si c'est sa... Exercice 1: Soit x_{0}=0 et x_{n+1}=x_{n}^{3} +\frac{1}{4} a) J'ai montré que 0\le x_{n}\le\frac{1}{2} J'ai fait :) b)Calc...
- 12 Nov 2006, 21:53
- Forum: ✯✎ Supérieur
- Sujet: Convergence...
- Réponses: 3
- Vues: 566
- 09 Nov 2006, 21:04
- Forum: ✯✎ Supérieur
- Sujet: Nombre complexe, petit bug...
- Réponses: 5
- Vues: 634
oui.... Mais... e^{i\phi}+e^{i\rho} = e^{i\frac{\rho+\phi}{2}}(e^{i\frac{\rho-\phi}{2}}+e^{i\frac{\phi-\rho}{2}}) = e^{i\frac{\rho+\phi}{2}} 2cos(\frac{\rho-\phi}{2}) et j'ai essayé de remplacer e^{i\frac{\rho+\phi}{2}} par sa forme trigonométrique , mais je n'aboutit pas Et dévellop...
- 09 Nov 2006, 16:52
- Forum: ✯✎ Supérieur
- Sujet: Nombre complexe, petit bug...
- Réponses: 5
- Vues: 634
Nombre complexe, petit bug...
Bonjours , voilà j'ai oublié comment faire quelques chose sur les complexes et cela m'embete beaucoup....
Calculer le module et l'argument de :

Je ne sais pas ...
Merci à vous :king2:
Calculer le module et l'argument de :
Je ne sais pas ...
Merci à vous :king2:
- 09 Nov 2006, 15:49
- Forum: ✯✎ Supérieur
- Sujet: Nombre complexe, petit bug...
- Réponses: 5
- Vues: 634
Géométrie...
Voila l'énoncé bête mais j'ai du oublié des propriété....
On a un cercle (C) de rayon R et on a trois point A, B ,C appartenant a (C) tel que l'angle ABC = 30°.
Démontrer que AC=R
Merci d'avance les Matheux!!
On a un cercle (C) de rayon R et on a trois point A, B ,C appartenant a (C) tel que l'angle ABC = 30°.
Démontrer que AC=R
Merci d'avance les Matheux!!
- 07 Nov 2006, 16:52
- Forum: ✎✎ Lycée
- Sujet: Géométrie...
- Réponses: 1
- Vues: 424
Je suis désolé mais alors la j'ai pas compris....
Car je ne vois comment démontrer que cela est vrai pour tout n...
Car je ne vois comment démontrer que cela est vrai pour tout n...
- 06 Nov 2006, 07:12
- Forum: ✯✎ Supérieur
- Sujet: Recurence ou Réflexion...?
- Réponses: 5
- Vues: 619
oui j'ai bien utiliser la récurence pour la première partie , et la seconde vient de 
Mais comment démontrer que :

Tout est la le problème... :lol5:
Mais comment démontrer que :
Tout est la le problème... :lol5:
- 05 Nov 2006, 22:00
- Forum: ✯✎ Supérieur
- Sujet: Recurence ou Réflexion...?
- Réponses: 5
- Vues: 619
- 28 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
