Forum de Mathématiques: Maths-Forum

Hello, La justification que v/E(u) est diagonalisable laisse beaucoup à désirer. Ici, le fait que E(u) est un sous-espace stable est important pour en déduire que la restriction a cet espace est encore un endomorphisme diagonalisable. Il y a quand même un argument à donner, par exemple celui du pol...

Bonsoir à tous, voici deux somme que je dois calculer..

Aide s'il vous plait

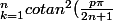et

Merci d'avance..

voici ce que j'ai dit..

Sachant que v est diagonalisable, et que sa restriction à tout espace propre de u E(u) est un endomorphisme, alors v/E(u) est diagonalisable.. Donc il existe une base de E(u) formée de vecteurs propres de v/E(u), qui sont eux meme vecteurs propres de v.

Est ce juste?

Bonsoir à tous, comment que ca va ? :zen: E est un K-ev de dimension finie, u et v deux endomorphismes diagonalisables de E qui commutent. 1- Montrer que tout espace vectoriel propre de u est stable par v. 2- Montrer que tout espace vectoriel propre de u admet une base formée de vecteurs propres pou...

Je remonte le sujet, je n'arrive pas la question 2/ b..

.. ou plutot je trouve quelque chose qui n'aboutit à rien..

Bonsoir, voici un exercice de Sup PCSI..



J'ai montré l'initialisation, mais je n'arrive pas à me lancer dans la question 2/ a..

De l'aide s'il vous plait..

Bonne soirée d'avance.

Bonsoir, voici un exercice que je fais en entrainement pour un ds.. http://img245.imageshack.us/img245/9764/img8108s.jpg 1ère question: u = -e_1-2.e_2+e_3 , g(e_2)=2.e_1+4.e_2-2.e_3 , g(e_3)=3.e_1+6.e_2-3.e_3 ==> c'est bon? d'où l'appartenance au vect qui se déduit facilement.. je bl...

tu dois regrouper tous les termes liés à un X de même degré ensemble.. (c'est la.....FACTORISATION ^^ )

Donc ici en regroupant les termes en X, tu a bien: (1-1)*X = 0*X = 0.

Bonsoir à tous, je suis en pcsi, et je me posait une question sur comment se servir, et surtout sur le sens meme de la relation liant coefficients et racines, régit par cette formule.. j'ai du mal à comprendre le principe.. [CENTER] http://upload.wikimedia.org/math/6/e/a/6ead91c29d0ccb13942472d3f1cf...

Bonjour à tous,

petite question toute bete, comment montrer que (en en fait..)

Merci d'avance

J'ai trouvé la solution avant hier, je donne les pistes pour ceux que ca pourrait interesser.. Il suffit de mettre au meme dénominateur.. En bas, on peut trouver un équivalent simple vu les facteurs du produit.. En haut, il faut faire 3 DL distincts (en faisant attentions aux ordres..), et on est ce...

Bonsoir à tous, a est une constante. On me demande de déterminer un équivalent le plus simple possible, ou à défaut la limite en 0 de: f(x)=\frac{1}{cos(x)-1}+\frac{2}{(e^{sh(x)}-1)^2}+\frac{a}{x} Je dois bien entendu utiliser le développement limité.. mais j'ai des s...

XENSECP a écrit:attention à la parité de n

La parité n'a rien à voir dans l'histoire, vu qu'il est positif.. si?

Bonjour à tous, voici un énoncé (je suis en PCSI) "Soit f un fonction dont le premier terme du DL(0) est en x^k ( k\geq1 ). A quel ordre suffit-il de pousser le DL(0) de f(x) pour obtenir un DL_n (0) de (f(x))^2 ?" Voila, j'ai pensé à un ordre \frac{n}{2} , car alors par co...

Bonjour, voila, il m'est demandé de : "Montrer que si f est injective alors pour toute partie A de E, f(\ complement\ de\ {A}\ ) \subset\ complement\ de\ f(A) " sachant que f va de E dans F... Help please.. J'ai le début: "Supposons f injective. Soit A = P(E), et et x ...

Bonsoir, Le problème c'est que l'affirmation du prof. est (évidement) vraie, mais il aurait dû rajouter que la réciproque est fausse. Par exemple l'intervalle [0,1[ de R admet une borne sup (qui est 1) mais pas de plus grand élément... Comment me faire comprendre quelque chose en deux phrases.. mer...

Bonjour à tous, je suis en pcsi, et j'aurais une question à propos du chapitre sur les corps réels... J'ai du mal à faire la différence entre "le plus grand élément de A", et "la borne supérieure de A".. En effet, d'après la définition vu en cours, j'ai: "a" plus grand ...

Bonjour à tous, et bonne année tout d'abord, voici un petit exercice sur les suites ( PCSI ): [INDENT] Pour n \geq 1 on pose a_n = (\frac{3}{4})^n.ln(n) et S_n = \bigsum_{k=1}^{n} \frac{ln k}{2^k} 1) Déterminer : \lim_{x \to \infty} a_n 2) En remarquant que pour tout n \geq 1 , S_n =...

une belle moustachue : http://moe.mabul.org/up/moe/2009/11/29/img-133454drveg.png De une tu ne répond pas à ma question, et de deux je suis aussi capable de tracer la courbe sur ma calculette, mais c'est vraiment faire preuve de bêtise que de se rattacher en permanence à une machine.. Je parle de l...

dudumath a écrit:il faut enlever à ton domaine les points où sin(théta)=1/2

pardon, j'ai modifié, en bas c'est du cosinus, pas du sinus.. du coup j'enleve les theta = Pi/3 + kPi et les 2Pi/3 + kPi