Forum de Mathématiques: Maths-Forum

Voilà j'ai fini !!
Mes résultats coïncides ^^

Merci beaucoup de m'avoir aidé, et de m'avoir aidé à comprendre mes erreurs :-)

annick a écrit:Passe d'abord par la forme exponentielle, quitte à revenir à la forme trigonométrique au final.

?

Soit 2 nombres complexes: 4${z_1} = {\rho _1}{e^{i{\theta _1}}} et 4${z_2} = {\rho _2}{e^{i{\theta _2}}} , alors: [CENTER] 5$ \red\frac{{{z_1}}}{{{z_2}}} = \frac{{{\rho _1}{e^{i{\theta _1}}}}}{{{\rho _2}{e^{i{\theta _2}}}}} = \frac{{{\rho _1}}}{{{\rho _2}}}{e^{i\left( {{\theta _1} - {\theta _2}...

Ah oui
En effet c'est mieux merci :we:

Il y a une erreur pour l'argument de z2. z_2=1-i lz_2l=\sqrt{{1^2}+{(-1)^2}}=\sqrt{2} cos\theta=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} sin\theta=\frac{-1}{\sqrt{2}}=\frac{-\sqrt{2}}{2} On peut prendra \theta=\frac{\pi}{4} z_2=\sqrt{2}(cos(\frac{\pi}{4})+isin(\frac{\pi}{4})...

z_1=\frac{{\sqrt{6}+i\sqrt{2}}}{2} z_2=1-i Donnez une forme trigonométrique de : z_1,z_2 et \frac{z_1}{z_2} J'ai trouvé z_1=\sqrt{2}(cos(\frac{\Pi}{6})+isin(\frac{\Pi}{6})) et z_2=\sqrt{2}(cos(\frac{\Pi}{4})+isin(\frac{\Pi}{4})) Pour la forme trigonom...

Ensuite j'ai un second exercice.
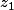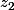J'ai et , il demande de trouver une forme trigonométrique de 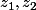(j'ai trouvé) et de . pour ce dernier je dois prendre les formes trigo que j'ai trouvé et les formes de départ ??

Un peu d'aide s'il vous plait ?

XENSECP a écrit:Par le module des complexes associés

Merci, je viens de me rendre compte que j'avais oublié ce passage ^^

Et bien, voilà, ça aussi c'est juste. Merci :we: Maintenant il me demande de placer les points A,B,C,D dans le repère. Je l'ai fait et il demande de démontrer que le quadrilatère OACB est un losange. Un losange est un quadrilatère qui a deux cotés consécutifs de même longueur. J'ai donc calculé BC ...

XENSECP a écrit:Calcule les cos et les sin, ce sont des valeurs classiques.

d = ?

annick a écrit:Ok, c'est juste.

Ok c'est déjà une bonne chose de faite.
Ensuite pour d sous forme algébrique.
J'ai la forme trigonométrique
Mais je ne sais pas comment passer de là, à la forme algébrique !

Bonjour, pour c, tu as : c=3/2+V3/2i= r(cost+isint) Que vaut alors rcost ? et rsint ? Met tout ça au carré, additionne et tu trouves r², donc r. Ensuite, ça te permet de calculer cost et sint et donc de trouver t et de mettre sous la forme exponentielle. Je trouve c = \sqrt{3}e^{i{\frac{\Pi}{6}}

XENSECP a écrit:Pour c c'est faux.

Pour d tu dois simplifier l'expression encore..

Désolé j'ai beau chercher mais je n'arrive pas à trouver ce qui est faux !

XENSECP a écrit:Hello,

Forme exponentielle c'est donc ce n'est pas bon pour la 1)

Pour c ou d ??

Parce que j'ai fait en fonction de mon cours !!

Bonjour, Je suis en TS et j'ai des exercices sur les nombres complexes avec des exponentielles, j'ai commencé mais je suis bloquée. Est ce quelqu'un pourrait m'aider s'il vous plait ? Ex: Le plan complexe est rapporté à un repère orthonormé direct (O,\vec{u},\vec{v}) (unité graphique 4 cm). ...

Pourais-je avoir une réponse s'il vous plait ?

Je suis bloquée à la dernière question de cet exercice. J'ai su des questions précédentes que f'(x) était croissante, qu'il existait un unique nombre alpha de I pour lequel f'(alpha)=0 (0.5<alpha<0.6) et que f(x) était croissante sur 0,alpha et décroissante sur alpha,pi/2. La question est: On note M...

Donc f"(x)=2+2cos²(x)-sin²(x)
(je vais y arriver ^^)

sin²(x)=sin(x)*sin(x) Donc (sin²(x))'=sin'(x)*sin(x)+sin(x)*sin'(x) (sin²(x))'=cos(x)*sin(x)+sin(x)*cos(x) (sin²(x))'=2sin(x)cos(x) Et tu peux reconnaitre une identité remarquable : c'est sin(2x). Ce n'était malheureusement ni l'un ni l'autre. Donc si je comprend bien f'(x)=2x-2+2sin(x)cos(x) et si...

Merci

Mais j'aurais encore quelques petites questions ^^ (juste vérification cette fois ci)

f(x)=(x-1)²+sin²(x)
donc
f'(x)=2x-2+cos²(x) ou f'(x)=2x-2+2cos(x)
et
f''(x)=2+sin²(x) ou f"(x)=2+sin(x)